Sudoku
Solitaire de nombres
Grilles
- Grilles du jour en mode texte ou à imprimer. Vous pouvez compléter les grilles sur place ou les recopier dans votre traitement de texte préféré. Vous pouvez obtenir et copier la solution à tout moment.
- Grilles du jour à imprimer uniquement
Règle de construction
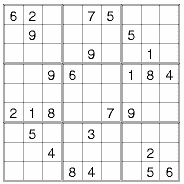
Vous pouvez aussi remarquer que cette grille est partagée en 9 régions (blocs ou boîtes) qui sont des carrés de 3 cases de côté, donc contenant 9 cases aussi.
Certaines de ces 81 cases contiennent déjà un nombre entier compris entre 1, le minimum autorisé, et 9 le maximum.
Vous devez compléter cette grille de telle manière que chaque ligne, chaque colonne et chaque bloc contienne tous les entiers de 1 à 9.
(Chaque entier figure une fois et une seule dans chaque ligne, dans chaque colonne et dans chaque bloc).
Cliquez sur l'image pour afficher le sudoku dans le tableau ci-dessous.
En passant la souris sur une case vide, vous faites apparaître au-dessous de la grille la liste des valeurs possibles (mais une seule de ces valeurs correspond à la solution cherchée).
Si vous n'arrivez pas à trouver la solution, cliquez sur le bouton [Solution].
Si vous désirez seulement une aide, en cliquant sur le bouton [Aide] vous obtiendrez les coordonnées (x, y) d'une case vide et un ou plusieurs nombres possibles pour cette case (qui sera automatiquement complétée s'il n'y a qu'une valeur possible).
Remarques
1) L'application ne donne que la première solution trouvée, même s'il y en a plusieurs.
2) Vous pouvez compléter une grille vide, le remplissage est une grille valide obtenue de manière aléatoire.
3) Vous pouvez entrer tous les jeux que vous trouvez dans des revues. Certains seront peut-être plus longs à résoudre que d'autres, (l'application est écrite en javascript).
4) Vous pourrez aussi essayer les exemples donnés dans cette page.
2) Vous pouvez compléter une grille vide, le remplissage est une grille valide obtenue de manière aléatoire.
3) Vous pouvez entrer tous les jeux que vous trouvez dans des revues. Certains seront peut-être plus longs à résoudre que d'autres, (l'application est écrite en javascript).
4) Vous pourrez aussi essayer les exemples donnés dans cette page.
Exemples
Très faciles
(Image),
1,
2,
3
Moins faciles
1
Difficiles
1,
solution.
Jeu
La grille
Outils
Générateur
Utilisation
Pour construire une nouvelle grille à compléter, [Nouvelle Grille] [Recommencer] [Afficher] [Résoudre].
Vous pouvez voir la chaîne se construire ci-dessous petit à petit.
Vous pouvez voir la chaîne se construire ci-dessous petit à petit.
Symétries
À l'origine, et c'est encore parfois le cas, les grilles proposées présentaient des symétries. Pour obtenir de telles grilles il suffit de modifier le générateur pour qu'il vide ou non les cases par groupes de plusieurs cases (deux pour une symétrie centrale ou axiale, 4 cases pour des rotations d'un quart de tour).
[Symétrie centrale] [Recommencer] [Rotations 1/4 tour] [Rec.] [Sym./Axes médians] [Rec.] [Sym./Diagonales] [Rec.]
[Afficher la grille]. [Résoudre].
[Symétrie centrale] [Recommencer] [Rotations 1/4 tour] [Rec.] [Sym./Axes médians] [Rec.] [Sym./Diagonales] [Rec.]
[Afficher la grille]. [Résoudre].
Algorithme
L'algorithme du générateur est le suivant :
1) a) Construction d'une grille complète de 81 cases. b) Choix d'un ordre de parcours des 81 cases.
2) Tout au long du parcours, on vide la case k et on résoud la grille incomplète, s'il y a plus d'une solution on replace l'élément dans la case k.
Vous remarquez à chaque étape deux nombres s'afficher, par exemple '32 28'. Dans cet exemple il reste 28 cases à parcourir et 32 ne sont pas vides, c'est donc que 32-28=4 nombres ont été replacés dans leur case.
Lorsque l'algorithme se termine l'affichage est par exemple '26 0', vous êtes certains que la grille a une soution unique, ce qui ne serait pas le cas si on enlevait l'un des 26 nombres restants. Évidemment une même grille complète peut éventuellement être obtenue à partir de grilles incomplètes différentes (lorsque l'ordre de parcours de l'algorithme change).
1) a) Construction d'une grille complète de 81 cases. b) Choix d'un ordre de parcours des 81 cases.
2) Tout au long du parcours, on vide la case k et on résoud la grille incomplète, s'il y a plus d'une solution on replace l'élément dans la case k.
Vous remarquez à chaque étape deux nombres s'afficher, par exemple '32 28'. Dans cet exemple il reste 28 cases à parcourir et 32 ne sont pas vides, c'est donc que 32-28=4 nombres ont été replacés dans leur case.
Lorsque l'algorithme se termine l'affichage est par exemple '26 0', vous êtes certains que la grille a une soution unique, ce qui ne serait pas le cas si on enlevait l'un des 26 nombres restants. Évidemment une même grille complète peut éventuellement être obtenue à partir de grilles incomplètes différentes (lorsque l'ordre de parcours de l'algorithme change).
Programme C
su_doku.c pour déterminer toutes les solutions. En entrée une chaîne du type 1--4--7-94--7 etc. En sortie les grilles pleines au format ascii.
Exemples
Les grilles à imprimer se trouvent dorénavant à la page : Grilles du jour
Codage en ligne
Vous pouvez entrer facilement certains sudoku trouvés sur le net ou que vous avez construit en effaçant au préalable la fenêtre d'aide ci-dessus ( exemple).
Cliquez ensuite ici.
(Les espaces " " et les fins de lignes sont ignorés, les chiffres 0 et les caractères autres que les chiffres de 1 à 9 doivent correspondre à des cases vides. Essayez avec le modèle
Inversement, vous pouvez obtenur le sudoku sous la forme d'une chaîne, en cliquant ici.
(Les espaces " " et les fins de lignes sont ignorés, les chiffres 0 et les caractères autres que les chiffres de 1 à 9 doivent correspondre à des cases vides. Essayez avec le modèle
1--4--7-94--7------8-----6-21------63----5-7---817-3----59-2-3-87--3-5----2-8----
Inversement, vous pouvez obtenur le sudoku sous la forme d'une chaîne, en cliquant ici.
Format d'affichage ASCII
Lorsque les signes
Inversement, après avoir entré le sudoku incomplet dans la grille plus haut, (exemple)), vous pouvez ensuite obtenir le sudoku au format ASCII en cliquant ici. (Donnez d'abord le signe zéro 0 , le point . ou l'étoile * que vous voulez utiliser pour représenter les cases vides).
-, +, servent de cadres et que les cases vides sont notées *, . ou 0,
cliquez ici.
Inversement, après avoir entré le sudoku incomplet dans la grille plus haut, (exemple)), vous pouvez ensuite obtenir le sudoku au format ASCII en cliquant ici. (Donnez d'abord le signe zéro 0 , le point . ou l'étoile * que vous voulez utiliser pour représenter les cases vides).
+-------+-------+-------+
| 1 . . | 4 . . | 7 . 9 |
| 4 . . | 7 . . | . . . |
| . 8 . | . . . | . 6 . |
+-------+-------+-------+
| 2 1 . | . . . | . . . |
| 3 . . | . . 5 | . 7 . |
| . . 8 | 1 7 . | 3 . . |
+-------+-------+-------+
| . . 5 | 9 . 2 | . 3 . |
| 8 7 . | . 3 . | 5 . . |
| . . 2 | . 8 . | . . . |
+-------+-------+-------+
Format LaTeX
Pour obtenir un fichier LaTeX complet de la grille (environnement picture), Cliquez ici.
Nombre de grilles
Équivalences
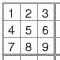
Outre cette permutation - sur place - des éléments, on peut [bouton B] permuter entre-elles les colonnes (et les lignes), à condition de conserver globalement les groupes de 3 colonnes (et ceux de 3 lignes, pour ne pas modifier le contenu global des blocs). On peut donc s'arranger pour que les trois éléments supérieurs de la 2ème boîte et ceux de la 3ème soient dans un ordre croissant. (4<6<9 et 5<7<8 sur l'image).
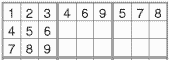
On peut encore [bouton C] permuter entre eux, en bloc, les trois groupements de trois colonnes (resp. lignes). On s'arrange donc pour que les deux derniers groupes de trois éléments de la première ligne soient placés dans l'ordre croissant (469 < 578 sur l'image) et on fait de même avec les deux derniers groupes de trois lignes (en lisant de haut en bas)
Autre transformation intéressante, la [bouton D] symétrie par rapport à la diagonale principale.
En définissant à partir de telles considérations une [bouton E] relation d'équivalence sur l'ensemble des grilles (en cliquant [E] vous obtenez n'importe quelle grille d'une même classe).
Toujours les mêmes grilles
Le [bouton E] vous permet d'obtenir un nombre impressionnant de grilles différentes à partir d'une seule.
En faisant le produit du nombre 362880 de permutations des 9 entiers du premier boc, par les 6^4 permutations à l'intérieur des 2ème et 3ème groupes de colonnes ou de lignes et les 2x2 permutations entre ces groupes, on obtient le nombre faramineux de 1 881 169 920 sudokus différents construits en partant d'un seul.
Êtes-vous réellement certain de ne pas acheter la même revue de sudoku semaine après semaine ? Avec juste un petit coup de [D] pour la rajeunir ! Espérons que non.
Que pensez vous de la publicité d'un jeu de sudoku dans laquelle on peut lire :
En faisant le produit du nombre 362880 de permutations des 9 entiers du premier boc, par les 6^4 permutations à l'intérieur des 2ème et 3ème groupes de colonnes ou de lignes et les 2x2 permutations entre ces groupes, on obtient le nombre faramineux de 1 881 169 920 sudokus différents construits en partant d'un seul.
Êtes-vous réellement certain de ne pas acheter la même revue de sudoku semaine après semaine ? Avec juste un petit coup de [D] pour la rajeunir ! Espérons que non.
Que pensez vous de la publicité d'un jeu de sudoku dans laquelle on peut lire :
Vous avez ue source infinie de grilles à votre disposition?
Dénombrement
En définissant une relation d'équivalence - de préférence la plus simple possible à utiliser - sur l'ensemble des grilles, il suffit de vérifier pour un seul représentant par classe si la grille est ou non un sudoku. Il ne reste qu'à multiplier par l'effectif des classes le nombre de grilles valides.
C'est le principe de la méthode utilisée par Bertram Felgenhauer et Frazer Jarvis qui indiquent le nombre 6670903752021072936960, c'est-à-dire plus de 6,67×1021 sudokus.
Ce nombre est celui de grilles
C'est le principe de la méthode utilisée par Bertram Felgenhauer et Frazer Jarvis qui indiquent le nombre 6670903752021072936960, c'est-à-dire plus de 6,67×1021 sudokus.
Ce nombre est celui de grilles
terminées, c'est-à-dire pleines et n'est pas le nombre de jeux que l'on peut vous proposer de compléter.
Quelques questions
On pourrait se poser la question de calculer le nombre de grilles incomplètes minimales (et qui se complètent de manière unique). Autre question, pour une grille donnée, quel est le nombre minimum de cases permettant de retrouver la grille complète (de manière unique). Le nombre de cas à étudier étant relativement limité, l'entreprise ne devrait pas être impossible.
On peut trouver à cette adresse des grilles incomplètes A de 17 nombres. Ces grilles n'ont qu'une solution, les résoudre n'est pas aisé et semble au delà des possibilités du javascript.
De plus, en définissant un degré de difficulté, on pourrait aussi déterminer les grilles les plus simples comme les plus compliquées à résoudre.
On peut trouver à cette adresse des grilles incomplètes A de 17 nombres. Ces grilles n'ont qu'une solution, les résoudre n'est pas aisé et semble au delà des possibilités du javascript.
De plus, en définissant un degré de difficulté, on pourrait aussi déterminer les grilles les plus simples comme les plus compliquées à résoudre.
Liens, références, documents, compléments
Dans un cube 8x8x8 vous devez compléter les 3x64 lignes parallèles aux arêtes et aussi 64 cellules 2x2x2 en utilisant chaque fois tous les huit entiers de 1 à 8.
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


