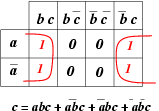Algèbre de Boole. Tableau de Karnaugh.

Écrivez une fonction des trois variables booléennes a, b et c.

Les variables sont 'a', 'b' et 'c'.
Les symboles de constantes sont '1' ou 'V' pour Vrai, '0' ou 'F' pour Faux.
'!' est l'opérateur unaire de complémentation (!a est le complément de a, on peut aussi utiliser les signes ?, -, /, \, N, n).
'+'  '.'   sont les opérateurs binaires de la somme et du produit booléens, le signe '.' peut être omis ou remplacé par x, *.
Les parenthèses '(', ')' ou les crochets '[', ']' peuvent être utilisés dans l'écriture de la fonction.

Expression booléenne

L'application construit le tableau de Karnaugh de la fonction booléenne et l'écrit sous forme normale disjonctive de la fonction. En outre l'application donne une expression simplifiée de la fonction.
Le tableau est prévu pour trois variables a, b, c. Si l'une des variables ou plusieurs d'entre elles sont absentes de l'expression, le nombre de cases du tableau et leur position ne changent pas et les trois variables peuvent apparaître dans la forme normale disjonctive.
La forme normale disjonctive est soit 0 soit une expression des trois variables a, b, c. C'est une somme d'au plus huit produits de trois facteurs. Les trois facteurs sont a, b, c ou leurs compléments !a, !b et !c. (Par exemple, un terme pourrait être a!b!c).
À chacun des termes de la forme normale disjonctive correspond une case du tableau et, inversement, à chaque case du tableau correspond un produit. (Par exemple, a!b!c se trouve dans la case définie par 'a' à gauche et par b!c! au-dessus).

Lorsque la fonction est constante égale à 0 ou à 1, le programme l'indique, Sinon une écriture simplifiée utilisant les variables a, b ou c est donnée.
Dans certains cas l'expression peut encore se simplifier, voir l'exemple par défaut où a.!b + !a.c + !b.c peut s'écrire a.!b + !a.c.
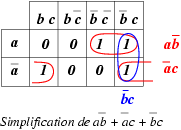
Lorsque le nombre de variables n'est pas élevé, le tableau de Karnaugh permet de simplifier assez simplement les expressions obtenues. L'image ci-contre montre comment simplifier a!b + !ac + !bc en a!b + !ac.
Les groupements considérés de plusieurs cases marquées '1' ont

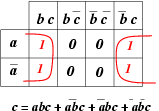
• 8 cases (toutes) : la fonction est égale à la constante '1'
• 4 cases (consécutives* ou en carré*) : le terme correspondant aux 4 cases est formé d'une seule variable ou de son complément
• 2 cases (accolées*) : le terme est composé de deux variables ( a !b par exemple).
• 1 case : les termes sont composés de trois variables (ou de leurs compléments)
• 0 case : la fonction est nulle.

* : sur le schéma, les deux cases !ac (en rouge) sont considérées accolées, de même dans un autre exemple on considèrerait que les 4 cases c = abc+a!bc+!abc+!a!bc forment un carré.

Remarques : Lorsque l'expression proposée est mal construite, certaines erreurs sont détectées, une expression vide et un caractère incorrect seront signalés ainsi que certaines erreurs de parenthèses ou de positions des opérateurs.
Si le tableau ne s'affiche pas, c'est que l'expression entrée est incorrecte et que le type de l'erreur n'a pu être déterminé.
Si vous voulez obtenir la forme normale conjonctive de f, cherchez la forme disjonctive de !f à l'aide de cette page et déduisez-en f = !(!f) à la main. par exemple avec f = a.(b+c)+!a.!c, calculez !f = !(a.(b+c)+!a.!c) = !a c + a !b !c et déduisez de cette dernière expression f = (a+!c)(!a+b+c) et vérifiez le résultat.

Expression booléenne