Accueil
Plan du site
Bloc notes
Jeux
Graphes
Combinatoire
Arithmétique
Algèbre
Analyse
Probabilités
Automates
Programmation
Divers
Liens
Home
Plan du site
Bloc notes
Jeux
Graphes
Combinatoire
Arithmétique
Algèbre
Analyse
Probabilités
Automates
Programmation
Divers
Liens
Home
Arithmétique Théorie des Nombres - Number Theory
| SOMMAIRE | Groupes | Pages Web | Associations | Projets | Pages Personnelles | Exercices |
| Problèmes | Conjectures | Demos | Images | Logiciels | Utilitaires | Ftp | C++ |
| Java | Théorie | ThÈses | Papiers | Journaux | Cours | Manuels | Historiques |
| Bibliographies | News | Questions | Liens |
| Problèmes | Conjectures | Demos | Images | Logiciels | Utilitaires | Ftp | C++ |
| Java | Théorie | ThÈses | Papiers | Journaux | Cours | Manuels | Historiques |
| Bibliographies | News | Questions | Liens |
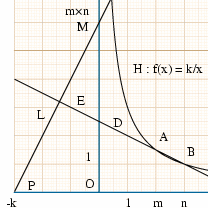
Produit de deux entiers et crible géométrique
Product and Geometric Sieve
GROUPES - GROUPS
www.mersenne.org George Woltman
This domain was created as a home for the Great Internet Mersenne Prime Search (GIMPS). Mersenne primes are named after the French monk Marin Mersenne. In his day, Marin Mersenne acted as great facilitator among the mathematicians and scientists of his day. In his honor, I am collecting links to math and science projects that you can participate in. You do not need to be a math or science whiz to join in the fun.
<http://www.mersenne.org/default.htm>
Les "recherches diophantiennes" regroupent des domaines de la théorie des nombres allant de la géométrie diophantienne à la transcendance de nombres, en passant par l'approximation par des nombres rationnels ou algébriques.
<http://www.math.unicaen.fr/dionet/>
PAGES WEB
Nombres premiers (crible, Construction d'une table, n-uplets de nombres premiers consécutifs de différences données, Nombres premiers probables ). Diviseurs. Ãcriture primaire. Nombres parfaits. Paires de nombres amiables. Suites aliquotes. Nombres pratiques (Déterminer si un nombre est pratique, Construction d'une table - en java - n-uplets de nombres pratiques de différences données, Table de nombres pratiques, Programme C). Flavius Josèphe, Suite de Syracuse, Suite de Fibonacci
<http://perso.wanadoo.fr/jean-paul.davalan/calc/arit/index.html>
Ce site très complet de Jean-Luc Garambois, présente tous les résultats connus sur les suites aliquotes et en particulier ceux obtenus par Jean-Luc Garambois, Cédric Barret, Olivier Huber et Matthieu Bachschmidt. Vous trouverez aussi les problèmes ouverts qu'ils soient théoriques ou des défis pour programmateurs.
<http://www.aliquotes.com/>
Created and maintained by Keith Matthews, Brisbane, Australia
<http://www.numbertheory.org/ntw/>
<http://www.dpmms.cam.ac.uk/Number-Theory-Web/web.html>
<http://www.utm.edu/research/primes/>
(from the Prime Pages' glossary)
<http://www.utm.edu/research/primes/glossary/BertrandsPostulate.html>
<http://www.mersenne.org/prime.htm>
<http://www.ics.uci.edu/~eppstein/numth/>
A search for ten consecutive primes in arithmetic progression
<http://www.ltkz.demon.co.uk/ar2/10primes.htm>
<http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Perfect_numbers.html>
This project is dedicated to all those who are fascinated by powers and integers.
<http://www.chez.com/powersum/>
The files in this directory summarize the state of the Cunningham project as of 29 July 1998.
<ftp://ftp.ox.ac.uk/pub/math/cunningham/>
<http://www-groups.dcs.st-and.ac.uk/~history/HistoryTopics.html>
<http://www.cecm.sfu.ca/projects/ISC/ISCmain.html>
FFT related stuff, the HFLOAT package & pi stuff
legal notice: Microsoft Network is prohibited from redistributing this work in any form, in whole or in part, without a license. License to distribute this work is available to Microsoft at $899. Transmission without permission constitutes an agreement to these terms.
<http://www.jjj.de/>
These are factorization results of various kind of numbers.
<http://www.asahi-net.or.jp/~KC2H-MSM/mathland/matha1/index.htm>
<http://www.asahi-net.or.jp/~KC2H-MSM/cn/>
<http://xraysgi.ims.uconn.edu:8080/amicable.html>
<http://home1.pacific.net.sg/~novelway/MEW2/perfect.html>
<http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Perfect_numbers.html>
(from the Prime Pages' glossary)
<http://www.utm.edu/research/primes/glossary/PerfectNumber.html>
<http://public.logica.com/~stepneys/cyc/p/perfect.htm>
Un papier sur les nombres n-adiques (certains de ces nombres sont appelés brenoms).
entiers de Gauss et autres textes.
<http://www.ens-lyon.fr/~vlefevre/math/index_fra.html>
Notes from Ed Eikenberg's talk on November 9, 2000
Let n be a positive integer. Does there exist a right triangle with rational sides whose area is n? If so, then n is called a congruent number. For example, the familiar 3-4-5 right triangle has area 6, so n=6 is a congruent number. But what about other values of n, like n=5 or n=157?
<http://www.math.umd.edu/~eve/cong_num.html>
<http://www.shef.ac.uk/~puremath/theorems/congruent.html>
<http://modular.fas.harvard.edu/Tables/elliptic_curves_in_nature/congruent_number_problem/>
WIFC Hisanori Mishima
These are factorization results of various kind of numbers.
MINT Multi-precision integer library - PPSIQS is the double large primes procedure variation of the self-intializing quadratic sieve. - factor Factorization program for general numbers.
<http://www.asahi-net.or.jp/~KC2H-MSM/mathland/matha1/index.htm>
Scott Contini
This is a web site dedicated to algorithms and computational results on integer factorization.
<http://www.crypto-world.com/FactorWorld.html>
<http://www.aliquot.de/aliquote.htm>
ASSOCIATIONS
<http://www.gnu.org/>Group Theory , Fields and Galois Theory, Algebraic Number Theory, Class Field Theory, Modular Functions and Modular Forms, Elliptic Curves , Algebraic Geometry, Lectures on Etale Cohomology, Abelian Varieties.
<http://www.jmilne.org/math/index.html>
PROJETS - PROJECTS
Goal. The original purpose of the ECMNET project was to make Richard's prediction true, i.e. to find a factor of 50 digits or more by ECM. This goal was attained on September 14, 1998, when Conrad Curry found a 53-digit factor of 2^677-1 c150 using George Woltman's mprime program. The new goal of ECMNET is now to find other large factors by ecm, mainly by contributing to the Cunningham project, most likely the longest, ongoing computational project in history according to Bob Silverman. A new record was set by Nik Lygeros and Michel Mizony, who found in December 1999 a prime factor of 54 digits using GMP-ECM
<http://www.loria.fr/~zimmerma/records/ecmnet.html>
PAGES PERSONNELLES - HOME PAGES
NTL: A Library for doing Number Theory (version 3.7a)
New York
<http://www.shoup.net/>
Hamburg
<http://agn-www.informatik.uni-hamburg.de/people/ehemalige/kassovic/dt.htm>
<http://www.numbertheory.org/ntw/number_theorists.html>
EXERCICES - EXERCISES
<http://www.vinc17.org/math/index_fra.html>Algorithms for Egyptian fractions
<http://www.ics.uci.edu/~eppstein/numth/egypt/>
<http://www.globetrotter.qc.ca/gt/usagers/sdesr/nb72.htm>
PROBLÈMES - PROBLEMS
<http://www.loria.fr/~zimmerma/problems/6174.html>CONJECTURES
<http://www.asahi-net.or.jp/~KC2H-MSM/mathland/overview.htm>Beal's Conjecture is this: There are no positive integers x,m,y,n,z,r satisfying the equation xm + yn = zr where m,n,r > 2 and x,y,z are co-prime (that is, gcd(x,y) = gcd(y,z) = gcd(x,z) = 1).
<http://www.norvig.com/beal.html>
If Ax +By = Cz , where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common factor.
<http://www.math.unt.edu/~mauldin/beal.html>
<http://www.bealconjecture.com/>
<http://www.primepuzzles.net/conjectures>
DEMOS
<http://www.cs.duke.edu/~mlittman/courses/Archive/cps130-97/animations/euclid.html> <http://users.erols.com/eweidaw/applets/EuclidExtension.html> <http://www.alpertron.com.ar/ECM.HTM>To determine linear integer dependence among numerical constants and to determine the minimal polynomial of an approximate algebraic number
<http://www.cecm.sfu.ca/projects/IntegerRelations/index.html>
IMAGES
chryzode.org - Un voyage en images dans la science des nombres (arithmétique) Les bottes de sept lieues du monde ondulatoire
Au carrefour de la recherche et des nouvelles technologies, les chryzodes (de chryzos et zooïde: écriture en or sur un cercle) nous font découvrir un monde foisonnant à peine exploré. Issus de la modélisation des nombres au moyen d'un cercle, ils nous renseignent aussi sur les structures, les résonances, les harmonies et les harmoniques des systèmes ondulatoires.
<http://www.chryzode.org/francais/intro.htm>
LOGICIELS - SOFTWARES
GMP is a free library for arbitrary precision arithmetic, operating on signed integers, rational numbers, and floating point numbers.
<http://www.swox.com/gmp/>
Tom St Denis
LibTomMath provides highly optimized and portable routines for a vast majority of integer based number theoretic applications (including public key cryptography). LibTomMath is not a cryptographic toolkit itself but it can be used to write one
<http://math.libtomcrypt.com/>
Calc c source files
<ftp://www.maths.uq.edu.au/pub/krm/calc/>
3branch 3x+1 3x+371 cfrac challenge convergents decimal discrete_log elliptic euclid factors fibonacci gcd ...
<ftp://www.maths.uq.edu.au/pub/krm/gnubc/>
<http://hasse.mathematik.tu-muenchen.de/ntsw/pari/Welcome>
<ftp://ftp.ox.ac.uk/pub/math/freelip/>
NTL: A Library for doing Number Theory (version 3.7a)
<http://www.shoup.net/ntl/>
<http://members.aol.com/~pg4dos/>
MIRACL: a Multiprecision Integer and Rational Arithmetic C/C++ library. This Portable C library implements a full implementation of Multiprecision Arithmetic. In particular it includes all the primitives necessary to implement Number Theoretic based methods for Public Key Cryptography and Digital signature, such as Diffie Hellman, Elliptic curves, RSA and DSS. Indeed example programs implement many of these methods.
<ftp://ftp.compapp.dcu.ie/pub/crypto/>
We are PSI, the algorithm company! PSI offers software, documents, books on the subjects of: compression, FFT, general transforms, wavelets, color graphics, Monte Carlo, fractals, convolution, signal processing, matrix algebra, genetic algorithms, number theory as used in factoring & cryptography.
giantint The giantint package consists of a library of routines for large integer arithmetic and number theory
<http://www.perfsci.com/>
<http://www.math.uga.edu/~ntheory/N1.html>
<http://rene.ma.utexas.edu/users/wfs/netmath/>
A C++ High Performance Arbitrary Precision Arithmetic Package
<http://www.jjj.de/mtommila/apfloat/>
OUTILS - TOOLS
Robert P. Munafo
With HyperCalc you can see that 27^86 is 1.251076x10^123, and 86! is 2.422709x10^130. Some calculators can handle that -- the current record-holder is AlCalc for the Pilot, which goes as high as 10^32767 and can handle 9274! (9274 factorial) But no other calculator can tell you that (27 ^ 86) ! = 10 ^ (1.534607.. x 10 ^ 125) or that 27 ^ (86!) = 10 ^ (3.467778.. x 10 ^ 130) (in other words, the first has over 10^125 digits and the second, with over 10^130 digits is "just a little bit" larger.)
<http://home.earthlink.net/~mrob/pub/perl/hypercalc.txt>
SITES FTP
Integer factorization using the Elliptic Curve Method
<ftp://ftp.loria.fr/pub/loria/eureca/tmp/GMP-ECM/>
C C++ code
NTL - MODULE: ZZ
The class ZZ is used to represent signed, arbitrary length integers.
Routines are provided for all of the basic arithmetic operations, as
<http://www.shoup.net/ntl/doc/ZZ.txt>
JAVA
<http://www.alpertron.com.ar/JAVAPROG.HTM>THÉORIE - THEORY
On the Integer Solutions of the Diophantine System
a1k + a2k + ... + amk = b1k + b2k + ... + bmk ( k = k1 , k2 , ... , kn )
<http://member.netease.com/~chin/eslp/eslp.htm>
Brigitte Vallée Université de Caen April 27, 1998 Summary by Cyril Banderier
<http://www-lipn.univ-paris13.fr/~banderier/Seminar/Vallee/>
THÈSES - THESIS
<http://www.numbertheory.org/ntw/N5.html>DOCUMENTS - PAPERS
<http://www.univ-tln.fr/~langevin/CDE/rsa.ps> <http://www.dpmms.cam.ac.uk/Number-Theory-Web/N4.html>Twenty years' analysis of the binary Euclidean algorithm Some parallel algorithms for integer factorisation Integer Factorization Algorithms Illustrated by the Factorization of Fermat Numbers
<http://web.comlab.ox.ac.uk/oucl/work/richard.brent/talks.html>
THE FIFTH SEMINAR ON THE MATHEMATICAL ANALYSIS of ALGORITHMS
Barcelona, June 14-18, 1999
<http://www.lsi.upc.es/~aofa/#participants>
Eamonn O'Brien - Groupes
<ftp://ftpmaths.anu.edu.au/pub/obrien/papers/>
article by Atkin and Bernstein
<http://pobox.com/~djb/papers/primesieves.dvi>
X.-D. JIA Southwest Texas State University Spring 1996
<http://www.math.swt.edu/~haz/prob_sets/notes/notes.html>
Finite and algebraic extensions Geometric constructions Splitting fields Irreducible polynomials over finite fields Quadratic reciprocity
<http://www.math.niu.edu/~beachy/aaol/fields.html>
by John A. Beachy
<http://www.math.niu.edu/~beachy/abstract_algebraII/>
<http://www.rzuser.uni-heidelberg.de/~hb3/rchrono.html>
Ilan Vardi IHES, Bures-sur-Yvette December 14, 1998
<http://algo.inria.fr/banderier/Seminar/Vardi/>
you should be somewhat familiar with the Fourier Transform and some elementary number theory (like modulo arithmetic)
<http://www.jjj.de/mtommila/ntt.html>
Andrzej Kondracki
<http://mizar.org/JFM/Vol9/wsierp_1.html>
Gauss proved that a regular n-gon could be geometrically constructed if the number of sides were a prime number of the form:Fn=2^(2^n))+1 where n is an integer Numbers of this form are also known as the Fermat numbers, they are not necessarily prime.
<http://www.geocities.com/RainForest/Vines/2977/gauss/formulae/gon17.html>
Some strongly undecidable natural arithmetical problems, with an application to intuitionistic theories.
Panu Raatikainen University of Helsinki, Finland
<http://projecteuclid.org/Dienst/UI/1.0/Journal?authority=euclid.jsl>
où l'on verra Ãratosthène, Fermat, Legendre, Gauss, Kraïtchik, Lehmer, Pollard, Lenstra et Pomerance se disputant à l'envi l'honneur du meilleur algorithme de factorisation
par Cyril Banderier,
<http://www-lipn.univ-paris13.fr/~banderier/Facto/facto.html>
<http://almira.math.u-bordeaux.fr:80/jtnb/jtnb.html>
(paru en TCS 257 (2001))
<http://www.logique.jussieu.fr/www.ressayre/jaf.dvi>
Bumby, Richard T.
<http://www.math.rutgers.edu/~bumby/squares1.pdf>
B.J. Green
<http://www.dpmms.cam.ac.uk/~bjg23/expos.html>
Cryptography Integer factorization, Faster arithmetic, More number-theoretic computations ...
D. J. Bernstein
<http://cr.yp.to/papers.html>
Ben Green, Terence Tao ((revised 9 Feb 2006)
<http://arxiv.org/abs/math.NT/0404188>
JOURNAUX - LETTERS
<http://www.numbertheory.org/ntw/N6.html>COURS - COURSES
Marc Hindry U. Paris Diderot PDF
congruences et corps finis, loi de réciprocité quadratique, cryptographie et test de primalité, codes correcteurs; équations diophantiennes, somme de carrés, Pell-Fermat, Fermat, anneaux d'entiers algébriques; fonction zeta et série L de Dirichlet, théorème de la progression arithmétique et théorème des nombres premiers.
Ce cours est publié en février (2008) chez Calvage & Mounet sous le titre "Arithmétique" . Ce livre contient en supplément un grand nombre d'exercices et deux chapitres (courbes elliptiques; développements et problèmes ouverts) ainsi que trois appendices (Factorisation, Introduction à la géométrie projective, Théorie de Galois).
Sur le site CultureMATH, lire l'Entretien avec Marc Hindry
<http://www.math.jussieu.fr/~hindry/enseignement_fr.html>
L'objectif n'est pas d'y proposer un cours d'arithmétique et les exercices correspondants mais de montrer à l'aide d'exemples d'exercices ou d'activités ce qui s'est fait dans nos classes.
Jean-Claude Renaud Lycée Louis Armand, Poitiers
<http://www.ac-poitiers.fr/math/prof/resso/arit/index.htm#sommaire>
<http://aquila.rezel.enst.fr/folium/algebre/arithmet/>
Pascal Boyer
<http://people.math.jussieu.fr/~boyer/fichiers/L2/cours.pdf>
<http://perso.wanadoo.fr/gilles.costantini/prepas.htm#gr>
D. Joyner and R. Kreminski
<http://tinah.mslab.usna.edu/docs/ebooks/book/book.html>
David R. Wilkins School of Mathematics, Trinity College, Dublin 2, Ireland
<http://www.maths.tcd.ie/~dwilkins/Courses/311/f>
ant.ps arith.ps algn.ps
<http://www.maths.ex.ac.uk/~rjc/rjc.html>
Selected from N4.html
Number Theory Web (Australian Site)
<http://www.maths.uq.edu.au/~krm/ntw/lecture_notes.html>
MANUELS - MANUALS
<http://www.shoup.net/ntl/doc/tour.html>HISTORIQUES - HISTORY
promenadesmaths.free.fr Frédéric Laroche
L'arithmétique, comme son nom l'indique (arithmos = ...), est l'étude des nombres. Les nombres sont...
<http://promenadesmaths.free.fr/histoire_arithmetique.htm>
<http://www.dpmms.cam.ac.uk/Number-Theory-Web/N14.html>
<http://www.math.uga.edu/~ntheory/N14.html>
RÉFÉRENCES - BIBLIOGRAPHIES
<http://www.rzuser.uni-heidelberg.de/~hb3/frecbib.html>GROUPES DE DISCUSSION - NEWS
The formula for 3 squares involves class numbers and is due to Gauss. He proved that for n > 3 the number R_3(n) of *primitive* representations as a sum of three squares is 12 h(-4n) for n = 1 or 2 (mod 4) and 24 h(-n) if n = 3 (mod 4) where h(-k) is the number of reduced positive definite binary quadratic forms of discriminant -k.
Robin Chapman
<http://www.math.niu.edu/~rusin/known-math/98/3squares>
QUESTIONS - POSTED
is close to zero for irrational x, of finding numbers such that ax^2+bx+c is close to zero (for a,b,c integers)?
<http://www.math.niu.edu/~rusin/known-math/95/algebraic.approx>
LIENS - LINKS
<http://www.dice.ucl.ac.be/~fkoeune/LLL.html> <http://www.math.uu.nl/people/vdkallen/lllimplementations.html> <liens_math.html> <liens_fermat.html> <liens_prime.html> <liens_combinat.html>Page de liens sur Catalan (et sur les nombres de Catalan)
<liens_catalan.html>
<liens_algebra.html>
<liens_crypt.html>
<http://www.math.uga.edu/~ntheory/number_theory.html>
| SOMMAIRE | Groupes | Pages Web | Associations | Projets | Pages Personnelles | Exercices |
| Problèmes | Conjectures | Demos | Images | Logiciels | Utilitaires | Ftp | C++ |
| Java | Théorie | ThÈses | Papiers | Journaux | Cours | Manuels | Historiques |
| Bibliographies | News | Questions | Liens |
| Problèmes | Conjectures | Demos | Images | Logiciels | Utilitaires | Ftp | C++ |
| Java | Théorie | ThÈses | Papiers | Journaux | Cours | Manuels | Historiques |
| Bibliographies | News | Questions | Liens |
| Accueil | Plan du site | Bloc notes | Jeux | Graphes | Combinatoire | Arithmétique | Algèbre |
| Analyse | Probabilités | Automates | Informatique | Divers | Lycée |
| Analyse | Probabilités | Automates | Informatique | Divers | Lycée |
Advertising :
If you see a reference in one of the files that is not linked, and you know of a link address to the appropriate document,
please send me mail, and I will include the link in the document. Thanks very much in advance.
Avertissement : Le classement par catégories est approximatif. Certains liens se retrouvent dans des rubriques différentes et sur plusieurs pages. Les commentaires sont généralement des courts extraits des pages référencées. Il est possible que certains liens nécessitent une mise à jour.
Tous commentaires ou remarques sont les bienvenus, vous pouvez les adresser à :

Les mises à jour demandées sont réalisées dès que possible et, sauf si c'est nécessaire, aucun message de réponse n'est expédié. Merci de m'écrire.
Copyright © 1999-2012 Jean-Paul Davalan - Reproduction interdite.
Avertissement : Le classement par catégories est approximatif. Certains liens se retrouvent dans des rubriques différentes et sur plusieurs pages. Les commentaires sont généralement des courts extraits des pages référencées. Il est possible que certains liens nécessitent une mise à jour.
Tous commentaires ou remarques sont les bienvenus, vous pouvez les adresser à :

Les mises à jour demandées sont réalisées dès que possible et, sauf si c'est nécessaire, aucun message de réponse n'est expédié. Merci de m'écrire.
Copyright © 1999-2012 Jean-Paul Davalan - Reproduction interdite.