Accueil / Arithmétique / Narcisse
Nombres narcissiques
Narcisse et les rondes des naïades, ses sœurs
Mythologie grecque
1) et 2) Selon "Les métamorphoses" d'Ovide
et d'autres sources, Narcisse est
un jeune homme d'une grande beauté qui repousse ses soupirantes dont la nymphe Echo
très éprise de lui. Ayant aperçu son reflet dans l'eau d'une source, il tombe amoureux de son image qu'il ne peut plus quitter du regard. Il dépérit et meurt.
À l'endroit de sa mort on vit éclore une fleur blanche.
3) Les nymphes éprises de la beauté d'Hylas qui puisait de l'eau dans une cascade, l'enlevèrent. Malgré ses recherches Héraclès ne put le retrouver.
Dans cette page on trouvera
1) des nombres qui sont identiques à leurs images dont ils ne peuvent plus se détacher, ce sont les nombres narcissiques. (370 en est un, vous en trouverez d'autres sur le graphe de cette page).
2) Les cercles des nymphes ou naïades, sœurs de Narcisse, seront alors ces cycles de nombres dont les images se reproduisent périodiquement (cherchez nymphe160, nymphe217 et nymphe352 sur le graphe de cette page, ou encore 136 et 244).
3) Tous les nombres restants seront attirés, en suivant les images successives, par l'un ou l'autre des k-cycles, comme jadis Hylas l'a été par un groupe de nymphes. (Jeu de piste : cherchez sur le graphe le chemin que parcourt Hylas115 jusqu'à la ronde de trois naïades qui l'aspire et l'engloutit).
3) Les nymphes éprises de la beauté d'Hylas qui puisait de l'eau dans une cascade, l'enlevèrent. Malgré ses recherches Héraclès ne put le retrouver.
Dans cette page on trouvera
1) des nombres qui sont identiques à leurs images dont ils ne peuvent plus se détacher, ce sont les nombres narcissiques. (370 en est un, vous en trouverez d'autres sur le graphe de cette page).
2) Les cercles des nymphes ou naïades, sœurs de Narcisse, seront alors ces cycles de nombres dont les images se reproduisent périodiquement (cherchez nymphe160, nymphe217 et nymphe352 sur le graphe de cette page, ou encore 136 et 244).
3) Tous les nombres restants seront attirés, en suivant les images successives, par l'un ou l'autre des k-cycles, comme jadis Hylas l'a été par un groupe de nymphes. (Jeu de piste : cherchez sur le graphe le chemin que parcourt Hylas115 jusqu'à la ronde de trois naïades qui l'aspire et l'engloutit).
Sommes digitales
Une transformation particulière
1) Prenez un nombre entier positif et écrivez sa décomposition décimale, par exemple N = 88593477.
Si N n'est pas nul vérifiez bien que le chiffre de gauche n'est pas un 0.
2) Comptez le nombre n de ses chiffres, dans l'exemple 88593477 est un nombre de n=8 chiffres.
3) Faites la somme T(N) de tous les chiffres élevés à la même puissance n :
T(N) = 8n +8n + 5n +9n +3n +4n +7n +7n que vous pouves encore écrire
T(N) = 2 ×88 + 58 +98 +38 +48 +2 ×78
T(N) = 2 ×16777216+390625+43046721+6561+65536+2 ×5764801
T(N) = 88593477
T(N) = N ⋅⋅⋅ bien entendu cela n'arrive que très rarement !
Vous ne retrouverez pas chaque fois votre nombre de départ. Si N a plus d'un chiffre et est choisi au hasard, la coïncidence sera même rarissime. L'algorithme T ci-dessus, transformera votre nombre N en un nombre T(N) le plus souvent différent du nombre N de départ.
Toutefois lorsque T(N) = N, votre N sera appelé nombre narcissique ou encore nombre plus que parfait et nombre d'Armstrong.
On démontre qu'il n'y a qu'un ensemble fini de nombres narcissiques, tous inférieurs à 1061. Les 88 nombres narcissiques non nuls ont tous été calculés. Le plus grand a 39 chiffres, en cliquant le bouton [Narcisse] de l'application, vous ferez apparaître l'un d'eux au hasard.
Entraînez vous ci-dessous à trouver des nombres narcissiques
2) Comptez le nombre n de ses chiffres, dans l'exemple 88593477 est un nombre de n=8 chiffres.
3) Faites la somme T(N) de tous les chiffres élevés à la même puissance n :
T(N) = 8n +8n + 5n +9n +3n +4n +7n +7n que vous pouves encore écrire
T(N) = 2 ×88 + 58 +98 +38 +48 +2 ×78
T(N) = 2 ×16777216+390625+43046721+6561+65536+2 ×5764801
T(N) = 88593477
T(N) = N ⋅⋅⋅ bien entendu cela n'arrive que très rarement !
Vous ne retrouverez pas chaque fois votre nombre de départ. Si N a plus d'un chiffre et est choisi au hasard, la coïncidence sera même rarissime. L'algorithme T ci-dessus, transformera votre nombre N en un nombre T(N) le plus souvent différent du nombre N de départ.
Toutefois lorsque T(N) = N, votre N sera appelé nombre narcissique ou encore nombre plus que parfait et nombre d'Armstrong.
On démontre qu'il n'y a qu'un ensemble fini de nombres narcissiques, tous inférieurs à 1061. Les 88 nombres narcissiques non nuls ont tous été calculés. Le plus grand a 39 chiffres, en cliquant le bouton [Narcisse] de l'application, vous ferez apparaître l'un d'eux au hasard.
Entraînez vous ci-dessous à trouver des nombres narcissiques
Calculez
Graphe orienté
Circuits et boucles
L'image ci-dessous représente un petite partie du graphe infini orienté G dont l'ensemble X des sommets est
l'ensemble des entiers naturels et dont l'ensemble des arcs est l'ensemble des couples N -> T(N)
de la transformation définie au paragraphe ci-dessus.
(Les sommets du schéma sont les naturels jusqu'à 137 inclus et tous les successeurs).
Vous remarquez sur l'image quelques boucles et quelques circuits (plus souvent appelés cycles en dehors de ce contexte de théorie des graphes).
Les boucles correspondent aux nombres narcissiques (SDI, sommes digitales invariantes).
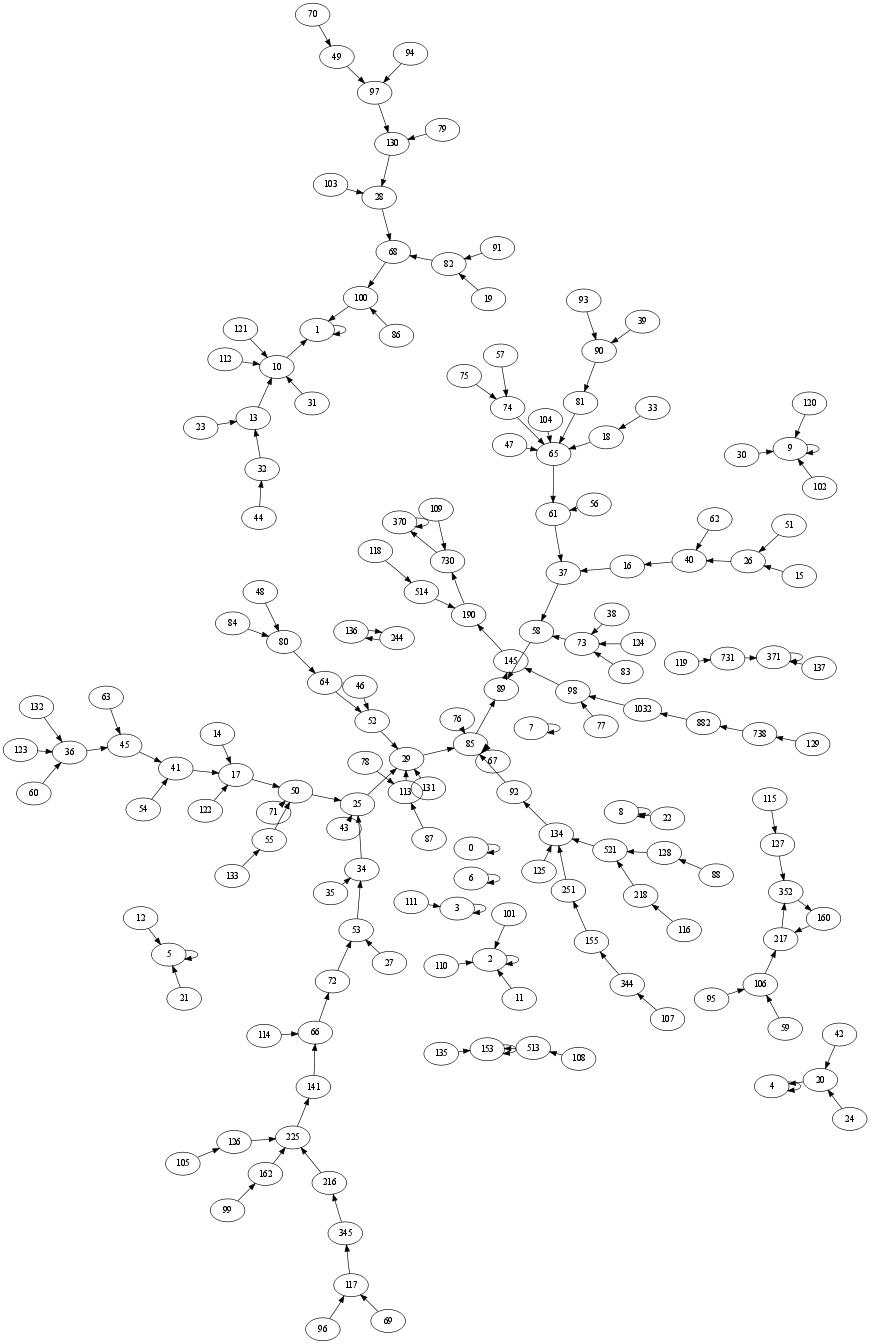
Détail d'une partie du graphe infini
(Les sommets du schéma sont les naturels jusqu'à 137 inclus et tous les successeurs).
Vous remarquez sur l'image quelques boucles et quelques circuits (plus souvent appelés cycles en dehors de ce contexte de théorie des graphes).
Les boucles correspondent aux nombres narcissiques (SDI, sommes digitales invariantes).

Vols finis
En partant d'un sommet de ce graphe et en suivant le chemin, par exemple : 70 → 49 → 97 → 130 → 28 → 68 → 100 → 1
on observe parfois des variations importantes en montées et descentes des valeurs des sommets 70 \ 49 / 130 \ 28 / 100 \ 1.
Pour tout sommet du graphe infini dont l'image ci-dessus n'en représente qu'une infime partie, il existe trois possibilités :
— il peut être une boucle, comme 1, 2, ...,9
— ou un sommet d'un circuit, comme 160, 217, 352
— ou, en partant de ce point, l'origine d'un chemin qui débouche sur un point fixe ou sur un élément d'un cycle, comme c'est le cas pour 69.
La démonstration (demo) de la finitude des nombres d'étapes, de points fixes et de circuits sera détaillée juste aorès l'application qui suit et qui peut aider à mieux comprendre.
Pour tout sommet du graphe infini dont l'image ci-dessus n'en représente qu'une infime partie, il existe trois possibilités :
— il peut être une boucle, comme 1, 2, ...,9
— ou un sommet d'un circuit, comme 160, 217, 352
— ou, en partant de ce point, l'origine d'un chemin qui débouche sur un point fixe ou sur un élément d'un cycle, comme c'est le cas pour 69.
La démonstration (demo) de la finitude des nombres d'étapes, de points fixes et de circuits sera détaillée juste aorès l'application qui suit et qui peut aider à mieux comprendre.
Calculs des vols
Les records de durée sont détenus par
69 et son correspondant 96 parmi les nombres à deux chiffres. 255, 282 et leurs correspondants 525, 552, 282, 822 parmi les trois chiffres. et ensuite par 5589, 11949 qui débouchen sur un circuit de 12 nombres de huit chiffres, (10156 n'est pas loin du précédent dont il emprunte aussi la majeure partie du trajet) et 40056, 368888, 3003688, 20223489, 10002999, etc.
69 et son correspondant 96 parmi les nombres à deux chiffres. 255, 282 et leurs correspondants 525, 552, 282, 822 parmi les trois chiffres. et ensuite par 5589, 11949 qui débouchen sur un circuit de 12 nombres de huit chiffres, (10156 n'est pas loin du précédent dont il emprunte aussi la majeure partie du trajet) et 40056, 368888, 3003688, 20223489, 10002999, etc.
Records de durées des vols
Cherchez sur le graphe les chemins qui vous conduisent en 17 étapes de 69 ou de 96 jusqu'à 370. Ce sont les plus longs obtenus en partant d'un entier de deux chiffres.
On cherche les durées des plus longs vols réalisés en partant des entiers naturels de n chiffres (n non nul) et en s'arrêtant au premier nombre narcissique ou au premier k-cycle rencontré.
Ces durées records sont indiquées par la suite
On cherche les durées des plus longs vols réalisés en partant des entiers naturels de n chiffres (n non nul) et en s'arrêtant au premier nombre narcissique ou au premier k-cycle rencontré.
Ces durées records sont indiquées par la suite
0, 17, 99, 109, 173, 199, 235, 257, 265, 279, 281, 285, 297, 301, 304, 317, 326, 359, 363 ...Les nombres à l'origine de ces vols records sont indiqués ci-dessous. 228 et 255 et tous les nombres obtenus en permutant leurs chiffres conduisent à des vols records de durée 99 (les deux vols empruntent très rapidement le même trajet, le 99-ième itéré 586 appartient à un 10-cycle.
1, 2, 3, 4, 5, 6, 7, 8, 9, 69, 228, 255, 5589, 11499, 40056, 368888, 3003688, 20223489, 25558888, 203557778, 2333335999, 30000003479, 100466666999, 124445555889, 1000023899999, 50055555677789, 111134788999999, 1001555688999999, 10025556777999999, 224455567889999999, 2002557777999999999
Résultats
Points fixes
La liste des nombres narcissiques (A005188) est connue depuis de nombreuses années. Voir les liens du bas de page.
Voici le calcul réalisé la première semaine de mars 2009 jusqu'à n=60 chiffres (plus de 60 serait inutile) de l'ensemble des nombres narcissiques et des k-cycles de périodes inférieures ou égales à 50. Ces valeurs se trouvent dans un fichier texte [liste]. Un certain nombre de ces k-cycles sont totalement nouveaux.
Le premier tableau donne les nombres narcissiques, le second donne les k-cycles.
Voici le calcul réalisé la première semaine de mars 2009 jusqu'à n=60 chiffres (plus de 60 serait inutile) de l'ensemble des nombres narcissiques et des k-cycles de périodes inférieures ou égales à 50. Ces valeurs se trouvent dans un fichier texte [liste]. Un certain nombre de ces k-cycles sont totalement nouveaux.
Le premier tableau donne les nombres narcissiques, le second donne les k-cycles.
# ------------- 1 ------------------ 1 : 1 2 : 2 3 : 3 4 : 4 5 : 5 6 : 6 7 : 7 8 : 8 9 : 9 10 : 153 11 : 370 12 : 371 13 : 407 14 : 1634 15 : 8208 16 : 9474 17 : 54748 18 : 92727 19 : 93084 20 : 548834 21 : 1741725 22 : 4210818 23 : 9800817 24 : 9926315 25 : 24678050 26 : 24678051 27 : 88593477 28 : 146511208 29 : 472335975 30 : 534494836 31 : 912985153 32 : 4679307774 33 : 32164049650 34 : 32164049651 35 : 40028394225 36 : 42678290603 37 : 44708635679 38 : 49388550606 39 : 82693916578 40 : 94204591914 41 : 28116440335967 42 : 4338281769391370 43 : 4338281769391371 44 : 21897142587612075 45 : 35641594208964132 46 : 35875699062250035 47 : 1517841543307505039 48 : 3289582984443187032 49 : 4498128791164624869 50 : 4929273885928088826 51 : 63105425988599693916 52 : 128468643043731391252 53 : 449177399146038697307 54 : 21887696841122916288858 55 : 27879694893054074471405 56 : 27907865009977052567814 57 : 28361281321319229463398 58 : 35452590104031691935943 59 : 174088005938065293023722 60 : 188451485447897896036875 61 : 239313664430041569350093 62 : 1550475334214501539088894 63 : 1553242162893771850669378 64 : 3706907995955475988644380 65 : 3706907995955475988644381 66 : 4422095118095899619457938 67 : 121204998563613372405438066 68 : 121270696006801314328439376 69 : 128851796696487777842012787 70 : 174650464499531377631639254 71 : 177265453171792792366489765 72 : 14607640612971980372614873089 73 : 19008174136254279995012734740 74 : 19008174136254279995012734741 75 : 23866716435523975980390369295 76 : 1145037275765491025924292050346 77 : 1927890457142960697580636236639 78 : 2309092682616190307509695338915 79 : 17333509997782249308725103962772 80 : 186709961001538790100634132976990 81 : 186709961001538790100634132976991 82 : 1122763285329372541592822900204593 83 : 12639369517103790328947807201478392 84 : 12679937780272278566303885594196922 85 : 1219167219625434121569735803609966019 86 : 12815792078366059955099770545296129367 87 : 115132219018763992565095597973971522400 88 : 115132219018763992565095597973971522401
Cycles
# ------------- 2 ------------------ 1 : 136 244 2 : 2178 6514 3 : 58618 76438 4 : 2755907 6586433 5 : 8139850 9057586 6 : 277668893 756738746 7 : 21914086555935085 37878721692554416 8 : 187864919457180831 375609204308055082 9 : 13397885590701080090 40091536165423401387 10 : 108493282045082839040458 183144838903847612823687 11 : 1553298727699254868304830 2307549584666787613389634 12 : 1588396116116684818933208 1662583586865233549781926 13 : 242402817739393059296681797 295849292210483378481950761 14 : 10049035073962232777012913675 14146559684641908727185026871 15 : 10622389873461838795139919502096 20921248349728532825757809753362 16 : 1411141399999358029488960346019160 2240239782870943967874495925085635 # ------------- 3 ------------------ 1 : 160 217 352 2 : 282595 824963 845130 3 : 2767918 8807272 5841646 4 : 180975193 951385123 525584347 5 : 3396705890823 6294418483143 3654709782417 6 : 255349823145519 447090882837630 321411732579837 7 : 13893231469464009318515397541007 13895416448792275685473829744915 14056081652489244496435933616913 # ------------- 4 ------------------ 1 : 10933 59536 73318 50062 2 : 27510477911590 47800729611562 28794385423806 36834169210461 3 : 1988938580054728 5146957705687367 2276352319249162 3745072497367240 4 : 129071530839696064382 347328549450841014962 237866180836931794379 357668536389162411710 5 : 169557221530718698042702 169562018671994452158988 338161213991248464720940 248945121317161275449387 # ------------- 5 ------------------ 1 : 3656948275943 5759076689801 6405584099531 5650346085989 6213095485028 2 : 1663709064090943716 4077790934430101361 2736510308762619339 2870463571149040395 2869264747464021138 3 : 1795245058188658603 1940006654627814913 2859065497110079396 5571576991631940457 4088047402918504546 4 : 119204730567652576196 220602798577821749852 248765172852935962841 247670499321072742964 330535042354805755595 # ------------- 6 ------------------ 1 : 2929 13154 4394 7154 3283 4274 2 : 2191663 5345158 2350099 9646378 8282107 5018104 3 : 22955961974580 73803590128032 32357226447319 24318257549352 27971919071792 94220062144011 4 : 110626217298381828545 146915855127127161329 229223750849314583096 347285156784769167782 139948607895288216203 365753356563451932671 5 : 18962820859504701211892 28978179990182148302144 37867673425925389700897 28498148899689232677881 39640140247078869683999 46142684925982472355170 # ------------- 7 ------------------ 1 : 1139785743 5136409024 3559173428 4863700423 1418899523 9131926726 7377037502 2 : 59906808718 90920874919 136095696124 571650873350 99312318232 71352591397 66814785298 3 : 2419253396913226 5564859798630665 4314122390900936 5561890395668808 4840861420987271 2766744975063429 3814368015105159 # ------------- 8 ------------------ # ------------- 9 ------------------ 1 : 1113928853354 3643890762383 3764461348892 3764592377975 5486860104254 1128275756843 1308860468429 4217390478269 5840462013812 2 : 1086767104665073071794069358 1087711604326152142799037806 1087239298652275489393232318 2171687973158060309621788895 1668615408129926023267489583 1647904917435001854832981579 2152805184049778117800849152 1144789403208407365062959581 1629003705428087305710293501 # ------------- 10 ------------------ 1 : 496 1009 6562 3233 259 862 736 586 853 664 2 : 180450907 564207094 440329717 468672187 369560719 837322786 359260756 451855933 527799103 857521513 # ------------- 11 ------------------ # ------------- 12 ------------------ 1 : 2689794 12783081 39326052 45130596 45579685 68505765 27073124 11602212 1680387 5299971 15250704 6611844 2 : 13216291 44733413 5981093 11743403 5908997 17347727 23131558 17571846 30442597 49340036 44870531 23070276 # ------------- 13 ------------------ 1 : 18963633035544997 52551389500766905 35876461872431926 21697619891079652 69477330558375418 21897923093961655 69228536582676925 38160589126493611 37909523382771553 36306344090162179 33637808638944484 25950934023321628 35624633319183334 # ------------- 14 ------------------ 1 : 329340 537059 681069 886898 1626673 1665667 2021413 18829 124618 312962 578955 958109 1340652 376761 2 : 10636207155096237927550 17810399355898537585315 29004806621022790911382 27798354257924032012720 18425671021807766709823 10745681722149970125328 18989387814955285091968 47884659771227634888553 11925507595333861127731 18399115705999414000444 44932379349757066271101 26699880941081568083608 30133760133393802432549 18344342589646448004016 # ------------- 15 ------------------ # ------------- 16 ------------------ # ------------- 17 ------------------ # ------------- 18 ------------------ 1 : 10074069541108119620821 18935428129475061827932 28415252997720554102092 27233895488449729771663 28470768372157693427350 10181976920394277400584 27852314084047558510219 10688610940325001073897 19553092616993382187366 36662895609794210663524 27211241280778321507795 10180397389391156436853 28388673910517178592951 29032929335610790615729 44371031395529147765128 18399103996082548276483 37841895989779904859691 64484670033935168320603 # ------------- 19 ------------------ # ------------- 20 ------------------ # ------------- 21 ------------------ # ------------- 22 ------------------ # ------------- 23 ------------------ # ------------- 24 ------------------ # ------------- 25 ------------------ # ------------- 26 ------------------ # ------------- 27 ------------------ # ------------- 28 ------------------ # ------------- 29 ------------------ # ------------- 30 ------------------ # ------------- 31 ------------------ # ------------- 32 ------------------ # ------------- 33 ------------------ # ------------- 34 ------------------ # ------------- 35 ------------------ # ------------- 36 ------------------ # ------------- 37 ------------------ # ------------- 38 ------------------ # ------------- 39 ------------------ # ------------- 40 ------------------ # ------------- 41 ------------------ # ------------- 42 ------------------ # ------------- 43 ------------------ # ------------- 44 ------------------ # ------------- 45 ------------------ # ------------- 46 ------------------ # ------------- 47 ------------------ # ------------- 48 ------------------ # ------------- 49 ------------------ # ------------- 50 ------------------
Quelques explications
Cycles et points fixes
On peut démontrer (demo) assez simplement
qu'il n'existe qu'un nombre fini de points fixes et de cycles. Le principe est simple, vous l'avez peut-être découvert en jouant avec l'application ci-dessus.
La seule partie de niveau bac est un exercice classique, une étude des variations d'une fonction permet de montrer qu'une équation possède une racine unique sur un intervalle.
Cette partie peut être mise momentanément de côté.
1) De tous les nombres N de n chiffres, c'est N = 999...9 qui a la plus grande image T(N), ce qui nous donne un majorant M de T(N).
Essayez ces nombres 999...9 et 6941690...49.
2) Si un nombre N a 61 chiffres ou plus, alors T(N) a moins de chiffres que N. En cliquant sur Hasard, si le nombre initial a plus de 60 chiffres, vous remarquez que les premiers successeurs sont de plus en plus courts
3) Si N a 60 chiffres ou moins de 60 chiffres, alors T(N) n'a pas plus 60 chiffres. En cliquant sur Long chemin, vous remarquez que les longueurs des nombres sont très variables mais restent limitées (pas plus de 60 chiffres dans tous les cas).
4) Au bout d'un nombre fini k d'étapes l'un des nombres N, T(N), T^2(N)=T(T(N)), T^3(N), ..., T^r(N), ... a 60 chiffres ou moins ainsi que tous ceux qui viennent encore après. La système se met dans un cycle ou aboutit à un point fixe.
La suite ci-dessous indique les changements dans les différences des nombres de chiffres n de N=10n-1 et n-k de son image T(N). De n=2 jusqu'à n=33, k=-1, N a un chiffre de moins que T(N), ensuite de n=34 jusqu'à n=60, k=0 le nombre de chiffres est le même. De n=61 à n=85, k=-1.
La dernière suite (9, 63, 282, ...) a pour terme général
Les recherches de points fixes et de cycles se font dans l'ensemble des nombres de 60 chiffres au plus. Il est donc préférable de rester dans un ensemble de 396704524155 et non 1060 éléments.
 A Recurring Digital Invariant variant
page qu'Éric Angélini consacre aux nombres narcissiques et aux k-cycles.
Vous y retrouverez à la fois des résultats et des liens vers d'autres pages web.
A Recurring Digital Invariant variant
page qu'Éric Angélini consacre aux nombres narcissiques et aux k-cycles.
Vous y retrouverez à la fois des résultats et des liens vers d'autres pages web.
C'est en voyant sa demande et en adressant un 5-cycle à Éric que j'ai su que Hans Havermann en avait obtenu un quelques jours auparavant.
 OEIS A005188 suite des nombres narcissiques.
OEIS A005188 suite des nombres narcissiques.
 Groupe sci.math Liste de discussion sur les nombres narcissiques. (cache)
Groupe sci.math Liste de discussion sur les nombres narcissiques. (cache)
 Hans Havermann s'est engagé dans une recherche systématique des k-cycles à partir des plus petits précurseurs, sa page de résultats Program: base-10 "cyclist" number search, by increasing digit-size est mise à jour périodiquement.
Hans Havermann s'est engagé dans une recherche systématique des k-cycles à partir des plus petits précurseurs, sa page de résultats Program: base-10 "cyclist" number search, by increasing digit-size est mise à jour périodiquement.
 Narcisse Wikipedia
Narcisse Wikipedia
 Nombres narcissiques NOMBRES - Curiosités, théorie et usages Gérard Villemin
Nombres narcissiques NOMBRES - Curiosités, théorie et usages Gérard Villemin
 Les nombres narcissiques Diophante
Les nombres narcissiques Diophante
 Nombre narcissique Récréomath
Nombre narcissique Récréomath
 Nombre narcissique Wikipédia
Nombre narcissique Wikipédia
 Perfect and PluPerfect Digital Invariants Scott Moore
Perfect and PluPerfect Digital Invariants Scott Moore
 Narcissistic Number Recurring digital invariant Mathworld
Narcissistic Number Recurring digital invariant Mathworld
 Narcissistic Numbers Harvey D. Heinz
Narcissistic Numbers Harvey D. Heinz
 Digital invariants Lionel Deimel's Farrago. Perfect digital invariant (or PDI) of order k in base b. Pluperfect digital invariant (or PPDI) in base b. Hyperperfect digital invariant (or HPDI) is a base-b PPDI. Observations and Theorems
Digital invariants Lionel Deimel's Farrago. Perfect digital invariant (or PDI) of order k in base b. Pluperfect digital invariant (or PPDI) in base b. Hyperperfect digital invariant (or HPDI) is a base-b PPDI. Observations and Theorems
 Armstrong numbers Dik T. Winter. A list of Armstrong numbers. An Armstrong numbers is a n-digit number such that the sum of the n-th powers of the n digits equals the number. This list has all Armstrong numbers for basis 2 to 14 and a number for basis 15 and 16.
Armstrong numbers Dik T. Winter. A list of Armstrong numbers. An Armstrong numbers is a n-digit number such that the sum of the n-th powers of the n digits equals the number. This list has all Armstrong numbers for basis 2 to 14 and a number for basis 15 and 16.
 Narcissistic number Armstrong number BrianShader
Narcissistic number Armstrong number BrianShader
 Narcissistic Number
Narcissistic Number
1) De tous les nombres N de n chiffres, c'est N = 999...9 qui a la plus grande image T(N), ce qui nous donne un majorant M de T(N).
Essayez ces nombres 999...9 et 6941690...49.
2) Si un nombre N a 61 chiffres ou plus, alors T(N) a moins de chiffres que N. En cliquant sur Hasard, si le nombre initial a plus de 60 chiffres, vous remarquez que les premiers successeurs sont de plus en plus courts
3) Si N a 60 chiffres ou moins de 60 chiffres, alors T(N) n'a pas plus 60 chiffres. En cliquant sur Long chemin, vous remarquez que les longueurs des nombres sont très variables mais restent limitées (pas plus de 60 chiffres dans tous les cas).
4) Au bout d'un nombre fini k d'étapes l'un des nombres N, T(N), T^2(N)=T(T(N)), T^3(N), ..., T^r(N), ... a 60 chiffres ou moins ainsi que tous ceux qui viennent encore après. La système se met dans un cycle ou aboutit à un point fixe.
La suite ci-dessous indique les changements dans les différences des nombres de chiffres n de N=10n-1 et n-k de son image T(N). De n=2 jusqu'à n=33, k=-1, N a un chiffre de moins que T(N), ensuite de n=34 jusqu'à n=60, k=0 le nombre de chiffres est le même. De n=61 à n=85, k=-1.
2, 34, 61, 86, 111, 134, 158, 181, 204, 227, 250, 272, 295, 317, 340, 362, 385, 407, 430, 452, 474, 496, 519, 541, 563, 585, 608, 630, 652, 674, 696, 719, 741, 763, 785, 807, 829, 851, 873, 895, 918, 940, 962, 984, 1006, 1028, 1050, 1072, 1116, 1138, 1160, 1182, 1204, 1226, 1248, ... 1094,Cette suite donne des indications sur les nombres de chiffres comparés de N et de T(N) et donc sur un aspect du graphe de la transformation T. L'effondrement est plus violent pour les grands nombres, cette suite permet de majorer le nombre d'étapes nécessaires pour passer d'un nombre N de n chiffres à une image Tr(N) de 60 chiffres ou moins.
Changement d'espace de travail
La somme digitale ne dépend pas de l'ordre des chiffres dans l'écriture du nombre
Il peut paraître profitable de se placer dans l'ensemble des écritures, à l'ordre près des chiffres, dont la taille a une croissance polynomiale de degré 10 et non exponentielle de base 10.
Deux nombres N1 et N2 de même longueur n et de mêmes chiffres, pas nécessairement placés dans le même ordre, ont la même image T(N1) = T(N2). Voir par exemple 55320147 et 25051743 .
Les nombres de naturels différents de n = 1, 2, 3, 4, 5, 6, 7, ... chiffres sont
Deux nombres N1 et N2 de même longueur n et de mêmes chiffres, pas nécessairement placés dans le même ordre, ont la même image T(N1) = T(N2). Voir par exemple 55320147 et 25051743 .
Les nombres de naturels différents de n = 1, 2, 3, 4, 5, 6, 7, ... chiffres sont
9, 90, 900, 9 000, 90 000, 900 000, 9 000 000..., 9×10n-1, ... (A052268)Les nombres de naturels à l'ordre près des chiffres est considérablement moindre, il n'est plus que de
9, 54, 219, 714, 2001, 5004, 11439, ..., binomial(n+9,9)-1, ...(A035927)Le quotient
a(n+1)/a(n) est proche de 1 + 9/n et tend vers 1 à l'infini alors que ce quotient est de 10 pour la première suite.
En cumulant les termes de la suite précédente, on obtient le nombre de multi-ensembles de n éléments au plus pris parmi les dix chiffres de 0 à 9, non tous des 0. C'est le nombre de manières de choisir les
chiffres pour former tous les naturels non nuls de n chiffres au plus.
9, 63, 282, 996, 2997, 8001, 19440, 43749, 92368, 184745, 352704, 646633, 1144052, 1961241, 3268744, 5311718, 8436267, 13123091, 20029990, 30044994, binomial(n+10,10)-n-1,..Ces deux dernières suites sont décrites à la page "Écritures décimales à l'ordre près des chiffres" qui a été écrite pour compléter celle-ci. On y trouve d'autres applications sur les nombres d'écritures des entiers, les nombres d'anagrammes de mots ou de nombres ainsi que des calculs de coefficients binomiaux ou multinomiaux sur des grands entiers.
La dernière suite (9, 63, 282, ...) a pour terme général
(n+10)(n+9)...(n+1)/10! -n-1 est polynomiale de degré 10
alors que la suite des nombres d'entiers naturels de n chiffres est (à une unité près) l'exponentielle 10n.
Pour cette raison, il est préférable de se placer dans l'ensemble indépendant de l'ordre des chiffres.
Connaissant les chiffres, mais pas leur ordre, d'un point fise ou d'un élément d'un cycle,
on retrouve les valeurs exactes du point fixe ou du cycle en calculant seulement les images.
Les recherches de points fixes et de cycles se font dans l'ensemble des nombres de 60 chiffres au plus. Il est donc préférable de rester dans un ensemble de 396704524155 et non 1060 éléments.
Crypto-narcisses
Les nombres crypto-narcissiques
Les nombres crypto-narcissiques doivent d'abord être codés avant d'effectuer la somme des puissances des chiffres. Le nombre 16797667 est l'un d'eux et le chiffrement consiste – pour lui – à prendre le complément à 9 de chaque chiffre. On obtient 83202332 qui a pour image le nombre de départ
Le chiffrement se fait cette fois en utilisant la permutation circulaire 0 → 9, 1&arr; 0 ...9 &arr; 8 vous permettra de vérifier que 26, 126, 217, 729, 729, 4193, 24228197, 93509953, 2491591748 sont bien des crypto-narcisses.
Pour quelle autre permutation circulaire des chiffres a t-on les crypto-narcisses 20, 40, 440, 532, 35484, 40608, 40609, 255083, 7598985478, 7598985479, 11395062344, 34544790113, 37508531533.
16797667, vérifiez-le. Un autre exemple qui utilise le même code : 369361709285.
Le chiffrement se fait cette fois en utilisant la permutation circulaire 0 → 9, 1&arr; 0 ...9 &arr; 8 vous permettra de vérifier que 26, 126, 217, 729, 729, 4193, 24228197, 93509953, 2491591748 sont bien des crypto-narcisses.
Pour quelle autre permutation circulaire des chiffres a t-on les crypto-narcisses 20, 40, 440, 532, 35484, 40608, 40609, 255083, 7598985478, 7598985479, 11395062344, 34544790113, 37508531533.
Comment décoder un crypto-narcisse ?
En partant d'un seul nombre, la tâche peut être ardue, mais
si vous avez toute une famille de crypto-narcisses de même code et que plusieurs d'entre eux n'ont que deux chiffres,
vous aurez rapidement des informations utiles.
Ce sera le cas avec la famille 25, 36, 37, 64, 16777476, 16777477, 98079206, 98079207, 5409060621, 5714384598, 63178121995, 596913056230.
On remarque que a) 25 = 5^2 + 0^2 = 3^2 + 4^2, b) 36 = 0^2 + 6^2, c) 37=1^2 + 6^2, d) 64 = 0 + 8^2, sont les seules décompositions de ces quatre nombres de deux chiffres en sommes de deux carrés.
Les égalités b) et c) entraînent 3 → 6, ainsi que 6 → 0 et 7 → 1.
Ensuite d) donne 4 &rarr 8 et dans a) on utilise nécessairement 25 = 3^2 + 4^2 donc 2 et 5 ont pour images 3 et 4 mais l'ordre d'association n'est pas connu.
16777476 se code donc en ?0111810 où un chiffre est inconnu. Ce chiffre est nécessairement différent de 0, 1, 3, 4, 6, 8, on essaie donc 2, 5, 7 et 9 et on s'aperçoit que seul 2 convient. On en tire 1 &arr; 2. Le nombre 16777477 n'apporte quant à lui aucun nouveau renseignement.
C'est déjà un bon début, on a une grande partie du code :
Ce sera le cas avec la famille 25, 36, 37, 64, 16777476, 16777477, 98079206, 98079207, 5409060621, 5714384598, 63178121995, 596913056230.
On remarque que a) 25 = 5^2 + 0^2 = 3^2 + 4^2, b) 36 = 0^2 + 6^2, c) 37=1^2 + 6^2, d) 64 = 0 + 8^2, sont les seules décompositions de ces quatre nombres de deux chiffres en sommes de deux carrés.
Les égalités b) et c) entraînent 3 → 6, ainsi que 6 → 0 et 7 → 1.
Ensuite d) donne 4 &rarr 8 et dans a) on utilise nécessairement 25 = 3^2 + 4^2 donc 2 et 5 ont pour images 3 et 4 mais l'ordre d'association n'est pas connu.
16777476 se code donc en ?0111810 où un chiffre est inconnu. Ce chiffre est nécessairement différent de 0, 1, 3, 4, 6, 8, on essaie donc 2, 5, 7 et 9 et on s'aperçoit que seul 2 convient. On en tire 1 &arr; 2. Le nombre 16777477 n'apporte quant à lui aucun nouveau renseignement.
C'est déjà un bon début, on a une grande partie du code :
remplacer 0 1 2 3 4 5 6 7 8 9
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
par ? 2 3 4 6 ? 4 3 0 1 ? ?
sur la deuxième ligne, il ne reste que 5, 7, 8, 9, à placer et 3, 4 à préciser (codes de 2 et 5). En tout moins d'une cinquantaine de possibilités, une bagatelle, avant de trouver la réponse.
Puzzles
Voici d'autres crypto-narcisses dont les codes ont été perdus, vous devez les reconstituer. Évidemment deux chiffres identiques ont
le même code, deux chiffres différents ont des codes différents, vous devez donc découvrir pour chaque famille, comme dans l'exemple, une permutation de {0, 1, 2, ..., 9}.
Chaque série utilise le même code.
Imprimez ou téléchargez les deux fichiers pdf contenant chacun 20 (familles de) crypto-narcisses et un minimum d'explications, les réponses sont inscrites aux bas des pages.
[Puzzles I ] (familles 1-20)
[Puzzles II ] (familles 21-40)
Chaque série utilise le même code.
| 1) 8464, 13600099, 812444335, 964646544 | 2) 10, 25, 152, 7074, 2829786, 219132703, 430271706, 7044850206, 9198493995, 19263597127, 39088991239 | 3) 41, 85, 267034, 288630727, 592488080, 909342070, 931429880, 35441937150 |
| 4) 540, 4354, 5112356, 787134968 | 5) 134, 134797, 18476772, 542076461, 1216303604, 1981692798, 8050458402 | 6) 1522, 4354, 6753, 324491, 766740, 2549723, 95130338 |
| 7) 81, 6754, 92124, 5159603, 866150177 | 8) 8994, 71083747, 84501731 | 9) 7073, 7074, 62450, 113762, 2548883, 2548884, 8063912, 154393316, 835351001, 7381170707 |
| 10) 775, 36200, 434705, 973516, 35758052 | 11) 701, 946, 2484, 10400, 7860043, 77064132, 4630937222, 4963935875, 10987454321, 40122206370 | 12) 6499, 10902, 36919, 95186, 17631075, 391871735, 644914308, 2622173674, 4242958102, 6038726274, 9251868526, 43983041569 |
Imprimez ou téléchargez les deux fichiers pdf contenant chacun 20 (familles de) crypto-narcisses et un minimum d'explications, les réponses sont inscrites aux bas des pages.
[Puzzles I ] (familles 1-20)
[Puzzles II ] (familles 21-40)
Crypto-cycles
Les crypto-cycles (ou crypto-naïades)fonctionnent suivant le même principe, vous devez déterminer le code pour pouvoir passer d'un entier a l'autre et parcourir le cycle : 3628415702, 4924106526, 8632901023 (le code est une rotation du type x |--> x+k [mod 10] sur 0, 1, ..., 9 )
Documents - références - compléments - liens utiles
C'est en voyant sa demande et en adressant un 5-cycle à Éric que j'ai su que Hans Havermann en avait obtenu un quelques jours auparavant.
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()



_160x160.jpg)
_200x126.jpg)

