Suite de Fibonacci
Nombre d'or

La relation de récurrence linéaire u(n)=u(n-1)+u(n-2) a pour équation caractéristique x²=x+1 ou encore x² - x - 1 = 0 de discriminant Delta = 5 et de racines a=(1-5^½)/2 et b=(1+ 5^½)/2 (b est le nombre d'or)
On a donc une formule explicite directe u(n) = A aⁿ + B bⁿ où A et B dépendent de u(0) et de u(1).

La suite de Fibonacci vérifie F(n) = (bⁿ - aⁿ) / 5^½
a=-0,618033988749894848... et b=1,618033988749894848...

Comme |a| = 0,618... < 1 , pour n suffisamment grand, F(n) est très proche de bⁿ / 5^½
Exemple : F(10) = 55 et b¹⁰ / 5^½ = 55.0036361

La suite de Fibonacci est proche d'une suite géométrique de raison b et pour n suffisamment grand, F(n+1) est proche de b F(n)
Exemple : F(10) = 55, F(11) = 89 et b × F(10)=88.9918693

On sait que b= (1+ 5^½)/2 vérifie b² = b+1 donc
b = 1 + 1/b = 1+1/(1+1/b) = 1+1/(1+1/(1+1/b)) = ...

Le nombre d'or est approché par les quotients successifs

F(n+1) F(n)  :   1 1    2 1    3 2    5 3    8 5    13 8 ...

D'ailleurs, en divisant par F(n+1) la relation F(n+2) = F(n+1) + F(n), on obtient F(n+2) / F(n+1) = 1 + F(n) / F(n+1) ou encore

F(n+2) F(n+1) = 1 +  1  F(n+1) F(n)

ce qui permet de montrer que l'on a bien les réduites successives du nombre d'or.
Calcul des termes F_n et des quotients de termes consécutifs.

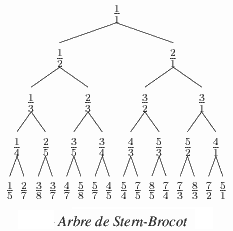L'arbre de Stern-Brocot représenté ci-contre en partie, contient toutes les fractions irréductibles strictement positives a/b, une seule fois chaque, et uniquement ces fractions. (Le numérateur a et le dénominateur b sont deux naturels premiers entre-eux).

Tout en haut de l'arbre, il faudrait placer la fraction 0/1 à l'extrême gauche et l'écriture (pas vraiment une fraction !) 1/0 à l'extrême droite.
L'arbre de Stern-Brocot se remplit en prenant les fractions intermédiaires de a/b au-dessus, immédiatement à gauche et c/d au-dessus à droite, tout simplement en additionnant les numérateurs d'une part, les dénominateurs d'autre part ce qui donne (a+c)/(b+d).

a) 3/2 s'obtient à partir de 2/1 et 1/1,
b) 5/3 à partir de 3/2 et 2/1,
c) 8/5 à partir de 5/3 et 3/2,
d) 13/8 à partir de 8/5 et 5/3,
e) 21/13 à partir de de 13/8 et 8/5 ...
f) F(n+1)/F(n) à partir de de F(n)/F(n-1) et F(n-1)/F(n-2) tout simplement car F(n+1) = F(n)+F(n-1) au numérateur et F(n) = F(n-1)+F(n-2) au dénominateur (et aussi qu'on a bien débuté en prenant 2/1 et 1/1, pour bien rédiger notre raisonnement par récurrence).
RLRLRLRLRLRLRLRLRL... est le mot infini associé au nombre d'or (R=Right="à droite", L=Left="à gauche").
Il suffit donc tout simplement de se déplacer alternativement à droite et à gauche en descendant l'arbre de Stern-Brocot pour obtenir la suite des réduites du nombre d'or et donc s'approcher de ce nombre d'or (tendre vers le nombre d'or).

du mot à la fraction

Inscrivez un mot dans l'alphabet {L,R} et découvrez la fraction associée.
RLRLRLRLRLRLRLRLRLRLRL

les quotients F_n+1/F_n ont pour limite b=1,618033988749894848... dont ils sont assez proches. Ce nombre b est lui même proche du rapport 1,609344 des mesures de distances en km et en milles terrestres (1 mille = 1,609344 km) ce qui permet des conversions approchées comme ci-dessous par qui connaît la suite de Fibonacci.

Approximations : 3 milles = 5 km, 5 milles = 8 km, 8 milles = 13 km, ... et plus généralement F_n milles = F_n+1 km

On peut aussi utiliser les nombres de Lucas - pas trop petits - comme dans 18 milles = 29 km.

Sur son site BLOGRUZ, Rémi Schulz recherche le nombre d'or et les termes de la suite de Fibonacci dans plusieurs oeuvres cinématographiques, dont le cuirassé Potemkine d'Eisenstein et dans le Conte d'été d'Éric Rohmer.
Il est aussi question dans ces pages de l'utilisation de la suite de Fibonacci par Pérec.

On lit ou on entend un certain nombre d'inepties sur le nombre d'or.
Une anecdote : la guide d'une abbaye de Provence affirmait que le nombre d'or égalait le rapport des côtés d'une feuille A4 (qui est la racine carrée de 2 et non le nombre d'or), l'exemple est mal choisi, mais ce n'est qu'une confusion plutôt amusante. Trouver le nombre d'or dans le règne végétal ou dans le règne animal serait tellement plus naturel !

Certaines élucubrations pseudo-scientifiques sont infiniment plus graves. Celles dénoncées sur cette page sont de ce type.