Accueil |
Index Graphes |
Cours BTS |
Circuit eulérien |
Plus court chemin |
Nombre chromatique |
Matrice de transition
Coloration d'un graphe
Nombre chromatique
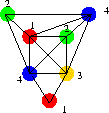 Colorier un graphe c'est colorier les sommets de telle façon que
deux sommets distincts et adjacents aient toujours des couleurs différentes.
Colorier un graphe c'est colorier les sommets de telle façon que
deux sommets distincts et adjacents aient toujours des couleurs différentes.
Le nombre chromatique est le plus petit nombre de couleurs nécessaires pour colorier le graphe.
Mathématiquement, c'est
1) donner un ensemble {1, 2, 3, 4, ..., n} de couleurs
2) une application surjective f de l'ensemble X des sommets vers l'ensemble des couleurs telle que pour tout arc ou arête (a, b) du graphe, f(a) soit différent de f(b), lorsque a différent de b.
Le nombre de couleurs est n.
Le nombre chromatique du graphe est la plus petit nombre possible de couleurs.
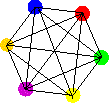
Il est facile de voir :
Si un graphe a n sommets, son nombre chromatique est inférieur ou égal à n.(Et donc si un graphe de n sommets a un sous-graphe complet de m sommets, alors son nombre chromatique est compris entre m et n).
(On peut donner des couleurs différentes aux sommets).
Si un graphe de n sommets est complet, alors son nombre chromatique est n.
(Deux sommets distincts devront avoir des couleurs différentes, il faut donc au moins n couleurs).
Si le plus grand degré d'un sommet est d, le nombre chromatique est inférieur ou égal à d+1.
(Prendre un sommet de degré d ainsi que les sommets qui lui sont reliés, colorier ces d+1 sommets avec d+1 couleurs différentes. Prendre ensuite, l'un après l'autre, les sommets restants ... pour chacun d'eux, l'une des couleurs, au moins, convient).
Algorithme glouton
Les couleurs sont numérotées 1, 2, 3 ... (Les couleurs sont les naturels non nuls).
1) Dresser une liste des sommets (généralement dans un ordre décroissant des degrés).
2) Tant que tous les sommets ne sont pas coloriés :
Choisir le premier sommet non encore colorié de la liste et lui affecter la plus petite couleur possible, (non déjà affectée à un sommet adjacent).
Remarque : En modifiant l'ordre des sommets de la liste, on peut parfois obtenir un nombre moindre de couleurs.
Cocher l'une des trois options définissant les constructions différentes de la liste des sommets.
1) Dresser une liste des sommets (généralement dans un ordre décroissant des degrés).
2) Tant que tous les sommets ne sont pas coloriés :
Choisir le premier sommet non encore colorié de la liste et lui affecter la plus petite couleur possible, (non déjà affectée à un sommet adjacent).
Remarque : En modifiant l'ordre des sommets de la liste, on peut parfois obtenir un nombre moindre de couleurs.
Cocher l'une des trois options définissant les constructions différentes de la liste des sommets.
Connaissant seulement les degrés des sommets, on peut obtenir une majoration du nbre chromatique :
Au cours de la recherche d'une coloration, en parcourant la liste des sommets, le nombre k de couleurs qui seront nécessaires est compris entre le nombre de couleurs utilisées et le plus grand degré +1 des sommets restant à colorier, ce qui permet de voir l'intérêt du classement dans l'ordre décroissant des degrés.
Lorsque le graphe est planaire, le nombre chromatique est inférieur ou égal à 4, c'est le cas de l'exemple ci-dessus.
* liste ordonnée l = 1 2 .. n des sommets, (nombre de sommets n)
* c(i-1) nb couleurs déjà utilisées avant le sommet i
* d(i) plus grand degré des sommets à partir de i
* nb chromatique C
pour i parcourant la liste des sommets de 1 à n
C <= max(c(i-1), 1+d(i))
En plaçant en début de liste les sommets dont les degrés sont les plus grands, on peut
minimiser la majoration
|
|
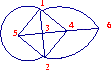
Au cours de la recherche d'une coloration, en parcourant la liste des sommets, le nombre k de couleurs qui seront nécessaires est compris entre le nombre de couleurs utilisées et le plus grand degré +1 des sommets restant à colorier, ce qui permet de voir l'intérêt du classement dans l'ordre décroissant des degrés.
Lorsque le graphe est planaire, le nombre chromatique est inférieur ou égal à 4, c'est le cas de l'exemple ci-dessus.
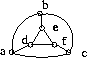
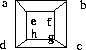
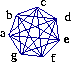
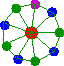
Exemples
Cliquez sur les images pour effectuer les calculs et déterminer des colorations.
Vous pouvez aussi modifier les données pour les adapter à d'autres exemples et chercher une coloration du graphe correspondant.
Vous pouvez aussi modifier les données pour les adapter à d'autres exemples et chercher une coloration du graphe correspondant.
Exemple initial
Graphe non orienté de nombre chromatique 2
Autres graphes non orientés
Liens
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()