Accueil/Jeux/Jeux logiques/Arcs-en-ciel
Arc-en-ciel
Graphe non-orienté multicolore
Schéma d'un graphe
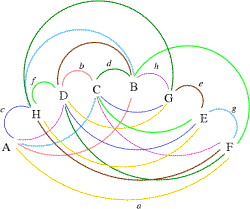
On se donne un graphe non orienté de n sommets A, B, C ... dont les arêtes sont coloriées par les n couleurs a, b, c ...
Un tel graphe se trouve sur le schéma ci-contre. Les arêtes sont coloriées de huit couleurs différentes nommées a, b, c ...
Vous trouverez aisément un cycle hamiltonien (passant par tous les sommets) de ce graphe.
Vous remarquerez peut-être que les arêtes de ce cycle hamiltonien sont toutes de couleurs différentes, si c'est le cas, ce cycle s'appelle un "arc-en-ciel".

Un tel graphe se trouve sur le schéma ci-contre. Les arêtes sont coloriées de huit couleurs différentes nommées a, b, c ...
Vous trouverez aisément un cycle hamiltonien (passant par tous les sommets) de ce graphe.
Vous remarquerez peut-être que les arêtes de ce cycle hamiltonien sont toutes de couleurs différentes, si c'est le cas, ce cycle s'appelle un "arc-en-ciel".
Tableau
Plutôt qu'un diagramme du graphe on préfère souvent dessiner un tableau, c'est ce qui sera fait systématiquement pour chaque graphe, dans la suite.
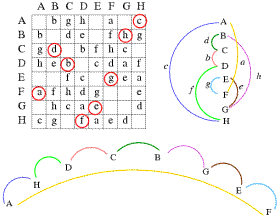
Chaque case vide du tableau indique qu'il n'y a pas d'arête entre les deux sommets indiqués dans les marges, à gauche et en haut du tableau. (Les lettres Majuscules sont utilisées pour les sommets).
Lorsqu'une case contient une couleur a, b, c ... c'est qu'il existe une arête entre les deux sommets et que cette arête a la couleur indiquée dans la case du tableau (sous la forme d'une lettre minuscule).
Comme le graphe est non-orienté, le tableau est symétrique. Chaque arête correspond à deux arcs d'orientations contraires (et de même couleur).
Le graphe proposé est sans boucles, la diagonale principale du tableau est vide. Le graphe est propre, (deux arêtes ayant une même extrémité sont de couleurs différentes), chaque ligne et chaque colonne du tableau ne contient pas deux fois la même lettre.


Chaque case vide du tableau indique qu'il n'y a pas d'arête entre les deux sommets indiqués dans les marges, à gauche et en haut du tableau. (Les lettres Majuscules sont utilisées pour les sommets).
Lorsqu'une case contient une couleur a, b, c ... c'est qu'il existe une arête entre les deux sommets et que cette arête a la couleur indiquée dans la case du tableau (sous la forme d'une lettre minuscule).
Comme le graphe est non-orienté, le tableau est symétrique. Chaque arête correspond à deux arcs d'orientations contraires (et de même couleur).
Le graphe proposé est sans boucles, la diagonale principale du tableau est vide. Le graphe est propre, (deux arêtes ayant une même extrémité sont de couleurs différentes), chaque ligne et chaque colonne du tableau ne contient pas deux fois la même lettre.
Arc-en-ciel
Les graphes proposés ici sont construits pour contenir au moins un cycle hamiltonien multicolore appelé "arc-en-ciel".
Jeu
Règle
La règle du jeu est de trouver un "arc-en-ciel".
Rien de plus simple ici, cliquez successivement sur certaines cases pour faire disparaître progressivement les arêtes jusqu'à obtenir n cases coloriées ou moins de couleurs différentes, au plus une par ligne et par colonne.
Avec un peu de chance vous aurez un cycle hamiltonien, sinon recommencez ou regardez la solution.
Pour simplifier la lecture du résultat, seul l'un des deux sens de parcours est affiché.
Attention, vous devez obtenir un seul cycle passant par tous les sommets et pas une réunion de deux cycles ou plus.
Rien de plus simple ici, cliquez successivement sur certaines cases pour faire disparaître progressivement les arêtes jusqu'à obtenir n cases coloriées ou moins de couleurs différentes, au plus une par ligne et par colonne.
Avec un peu de chance vous aurez un cycle hamiltonien, sinon recommencez ou regardez la solution.
Pour simplifier la lecture du résultat, seul l'un des deux sens de parcours est affiché.
Attention, vous devez obtenir un seul cycle passant par tous les sommets et pas une réunion de deux cycles ou plus.
Application
Lorsque vous cliquez dans une case (X, Y) du tableau contenant une lettre x, c'est que vous ne gardez que cet arc (X, Y) dans la couleur x.
L'application est capable d'en déduire un certain nombre d'actions qui consistent toutes à éliminer des arcs qui ne peuvent pas apparaître dans l'arc-en-ciel, compte tenu des choix précédents.
Deux niveaux sont proposés, cochez la case "Effectue toutes les simplifications possibles" pour effectuer un maximum les déductions. Vous pouvez annuler vos choix, dans l'ordre inverse, sauf si vous consultez la solution. Vous pouvez aussi revenir à la grille de départ, tant que vous ne changez pas de grille.
L'application est capable d'en déduire un certain nombre d'actions qui consistent toutes à éliminer des arcs qui ne peuvent pas apparaître dans l'arc-en-ciel, compte tenu des choix précédents.
Deux niveaux sont proposés, cochez la case "Effectue toutes les simplifications possibles" pour effectuer un maximum les déductions. Vous pouvez annuler vos choix, dans l'ordre inverse, sauf si vous consultez la solution. Vous pouvez aussi revenir à la grille de départ, tant que vous ne changez pas de grille.
Grilles en mode texte.
1) Cliquez ici ou encore là pour afficher cinq nouvelles grilles et leurs solutions ou pour les effacer.
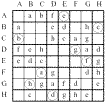
Grilles à imprimer.
1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 .
Sur le site
Documents, compléments, liens
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


