Plus court chemin dans un graphe non orienté
Recherche du plus court chemin
Algorithme de Dijkstra.
Les sommets du graphe non orienté et sans boucles, sont A, B, C, ..., H
Le programme va déterminer la valeur du plus court chemin entre deux sommets donnés du graphe, tout en détaillant la progression des calculs, permettant ainsi de comprendre l'algorithme utilisé.
Entrez les valeurs positives associées des arêtes du graphe. (lorsqu'il n'y a pas d'arête entre deux sommets laissez la case
vide).
Plus bas dans la page, plusieurs exemples de graphes sont dessinés et préprogrammés, en peu de clics, sans rien écrire, ils sont exécutés, la figure permet de visualiser la solution obtenue du plus court chemin.
Remarques
Si on ne modifie pas les données, ce programme permet en particulier de résoudre l'activité 11 (page 276 du livre de Maths de T.E.S.), dont
le graphe est représenté sur la première des figures visibles ci-dessous. D'autres exercices sont disponibles en cliquant.
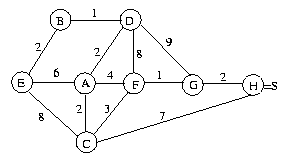
En changeant les données, lorsque le nombre de sommets du graphe ne dépasse pas 8, cette page permet de résoudre n'importe quelle
recherche de plus court chemin.
Liens
Plus court chemin Graphes, orientés ou non, d'un nombre quelconque de sommets.
L'algorithme est de Dijkstra.
Edsger Dijkstra est né à Rotterdam en 1930 et est décédé il y a moins de deux mois, le 6 Août 2002.
|
|
|
En France l'algorithme est attribué conjointement à Moore et à Dijkstra et est appelé « algorithme de Moore-Dijkstra ».
J. Strother Moore enseigne à l'université d'Austin au Texas.
J. S. Moore est avec Robert Stephen Boyer l'un des auteurs de NQTHM, un programme permettant de démontrer des théorèmes.
Boyer et Moore sont aussi les inventeurs de l'algorithme le plus rapide connu de
recherche de sous-chaînes
dans une chaîne de caractères (recherche des occurrences d'un mot dans un phrase ou dans un texte).
Faites Ctrl-F (ou Alt-F avec Netscape 4.7), dans la fenêtre
qui s'ouvre écrivez un mot, lancez ensuite sa recherche dans cette page, à ce moment là vous utilisez sans doute l'algorithme de Boyer-Moore.
|
|
|
