Fibonacci magique
Devinez le nombre choisi
Matériel
Il s'agit d'une variante à la Fibonacci-Zeckendorf d'un tour qui
utilise habituellement l'écriture binaire du nombre à deviner.
Commencez par imprimer la page au format pdf où sont représentées les cartes.
Vous pouvez ensuite découper ou non les dix cartes contenant des nombres de 1 à 100.
(Cartes dans le fichier : fibonacci.pdf).
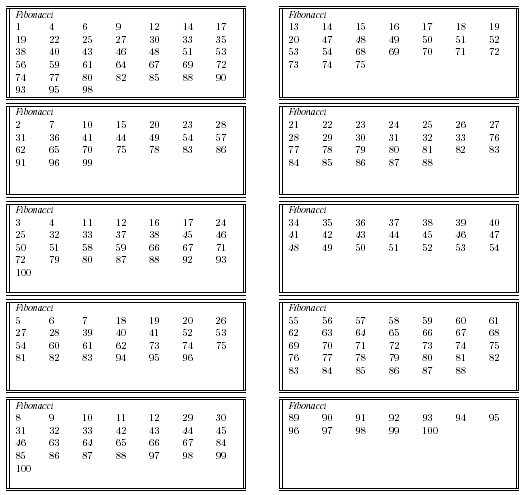
Cliquez sur l'image pour changer de méthode ou choisissez : Fibonacci, Lucas, binaire.
Commencez par imprimer la page au format pdf où sont représentées les cartes.
Vous pouvez ensuite découper ou non les dix cartes contenant des nombres de 1 à 100.
(Cartes dans le fichier : fibonacci.pdf).

Cliquez sur l'image pour changer de méthode ou choisissez : Fibonacci, Lucas, binaire.
Un nombre à deviner
Le tour est très simple : vous allez devoir deviner un nombre entier.
Demandez à une personne de l'assistance de penser à un nombre entier entre 1 et 100, sans vous donner la valeur de ce nombre.
Présentez à cette personne, successivement, les cartes en lui demandant de vous indiquer celles où figure le nombre.
Demandez à une personne de l'assistance de penser à un nombre entier entre 1 et 100, sans vous donner la valeur de ce nombre.
Présentez à cette personne, successivement, les cartes en lui demandant de vous indiquer celles où figure le nombre.
Solution
Additionnez les premières valeurs des cartes sélectionnées, vous retrouverez le nombre choisi.
Exemple : Le nombre 100 se trouve sur trois cartes. En haut et à gauche de ces cartes sont inscrits 3, 8 et 89 dont la somme est justement : 100 = 3 + 8 + 89 = F4 + F6 + F11.
Explication : Le système de numération utilisé est la représentation de Zeckendorf des nombres entiers positifs. Ceux-ci s'écrivent de manière unique comme sommes de nombres de Fibonacci Fi (dont les rangs i>1 diffèrent entre eux d'au moins deux unités).
Pour obtenir la décomposition d'un naturel, soustrayez successivement les plus grands nombres de Fibonacci possibles.
Exemple : Le nombre 100 se trouve sur trois cartes. En haut et à gauche de ces cartes sont inscrits 3, 8 et 89 dont la somme est justement : 100 = 3 + 8 + 89 = F4 + F6 + F11.
Explication : Le système de numération utilisé est la représentation de Zeckendorf des nombres entiers positifs. Ceux-ci s'écrivent de manière unique comme sommes de nombres de Fibonacci Fi (dont les rangs i>1 diffèrent entre eux d'au moins deux unités).
Pour obtenir la décomposition d'un naturel, soustrayez successivement les plus grands nombres de Fibonacci possibles.
Variantes du jeu
Suite de Lucas
Jeu classique
Les cartes utilisées généralement pour ce jeu sont basées sur l'écriture binaire du nombre entier.
(Cartes dans le fichier : binaire.pdf).
Que remarque-t-on lorsqu'on compare les cartes de Fibonacci ou de Lucas à celles jeu binaire habituel ?
(Cartes dans le fichier : binaire.pdf).
Que remarque-t-on lorsqu'on compare les cartes de Fibonacci ou de Lucas à celles jeu binaire habituel ?
Voir également
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


