Suite de Fibonacci
Fibonacci modulo - Nombres de Pisano - Bracelets

L'entier naturel m>0 étant donné, la suite des F(n) mod m est périodique, la suite obtenue est A001175 de N. J. A. Sloane. Voir à ce propos :
Periods of Fibonacci Sequence Modulo m et Find the Period of F(mod m) de Marc Renault,
Période du générateur de Fibonacci Pierre L. Douillet les générateurs uniformes
Periods of Fibonacci Sequences Mod m Math Pages - Kevin Brown
Pisano Number de Eric Weisstein's World of Mathematics.

Nombres de Pisano

Périodes des suites, modulo m, de Fibonacci, Lucas ou autres :
u(n+1) = u(n) + u(n-1)

u(0) =      u(1) =      modulo max =     
périodes suivant m = 2 .. max

Comportement des suites de type Fibonacci, modulo 10 : The Number Bracelets Game - Susan Addington    How long (or short) a number bracelet can you make?

Il s'agit de construire un bracelet de perles choisies parmi 10 couleurs : c(0), c(1), c(2) = c(0)+c(1) modulo 10, ..., c(n+1) = c(n)+c(n-1).
Après avoir déterminé une période, on en fait un bracelet.
Quelles sont les périodes, les bracelets ?


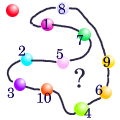Sur la figure ci-contre, le modulo (et le nombre de couleurs possibles) est 11 et non 10. Peut-on construire un bracelet de Fibonacci de 11 couleurs ?

En généralisant (le modulo n et les deux premiers termes quelconques), on peut chercher à dénombrer les bracelets constructibles par cette même récurrence c(n+1) = c(n)+c(n-1).

La suite A015134 de N. A. Sloane donne les nombres de périodes des suites de type Fibonacci, chacune étant définie à une rotation près.

Ci-dessous, on retrouve ces valeurs de cette suite et les différents bracelets constructibles :

Bracelets

Nombre de couleurs :   

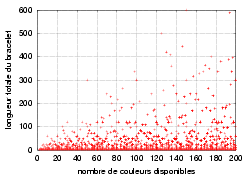
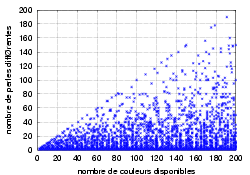
Nombres de perles des bracelets
Longueur totale du bracelet	Couleurs distinctes uniquement

à compléter ...

Un autre moyen de mettre en évidence graphiquement les périodes des suites modulo m, est de dessiner les points de coordonnées (F(n-1), F(n)) (modulo l'entier m).
Il est inutile de tracer plus de points que la longueur de la période (voir plus haut).
Essayez plusieurs valeurs de m.

Par exemple m=5, m=15, m=25, m=50, m=100, m=150, m=200, m=250.
Essayez de trouver de belles images, m=65, m=82, m=85, m=170, m=210, m=227, m=246.
Terminons avec m=370 (pour faire plaisir à ceux qui adorent faire scintiller un maximum d'étoiles).
Pour m donné, on peut déterminer tous les diviseurs d de m et calculer toutes les périodes des suites modulo d et comparer aux nombres de motifs des figures.
Lire les textes référencés plus haut au paragraphe des nombres de Pisano.
Remarques :

L'image est un carré de 500 pixels de côté, il est donc préférable que m ne dépasse pas la valeur 500. (Comment doit-on interpréter la figure obtenue en faisant m=2405 ?)
Les points bleus de la figure sont des carrés de 1 à 4 pixels de côtés selon la valeur de m, (pour m< 500, les points ne se chevauchent jamais).
Le nombre de points calculés et tracés a été volontairement limité, il sera inférieur à 60000, quelle que soit la période.

En choisissant d'utiliser, par exemple, la période 0 1 1 2 3 0 3 3 1 4 0 4 4 3 2 0 2 2 4 1 de la suite de Fibonacci modulo m=5, on se déplace d'une distance de 0, 1, 1, 1, 2, 3 ... pas, en pivotant chaque fois d'un quart de tour (1/4) entre deux déplacements consécutifs.
Le point de départ est représenté par le disque rouge, le point d'arrivée est le disque vert, le chemin parcouru est en bleu.
Il arrive parfois que les points de départ et d'arrivée soient confondus, ce n'est pas toujours le cas.
On peut décider de choisir de pivoter d'un autre angle, par exemple d'un tiers de tour (1/3) au lieu d'un quart de tour ou d'un autre angle.
La figure obtenue s'appelle en anglais spirolateral. Elle a été inventée en 1973 par le biochimiste britannique Frank C. Odds.
Le texte THE ART OF SPIROLATERAL REVERSALS par Robert J. Krawczyk vous donnera un aperçu des figures que l'on peut obtenir.
Marc S. Renault étudie ces graphes dans le même contexte des suites de Fibonacci.

Introduisez les deux premiers termes u0 u1 de votre suite et la valeur de m.
La touche [Aléatoire] choisit aléatoirement, à votre place, les trois nombres.
Les deux touches [--] et [++] permettent de modifier la valeur du modulo m.
Les deux applets des couples et des spirolaterals donnent simultanément les résultats correspondants aux mêmes valeurs de u0 u1 et de m. Il suffit de modifier les données dans l'un ou l'autre des deux.
On peut aussi changer aléatoirement les coefficients de la suite ou leur redonner leurs valeurs initiales 1 et 1 des suites de Fibonacci et de Lucas.
Quelques exemples Ex. 1, Ex. 2, Ex. 3, Ex. 4, Ex. 5, Ex. 6, Ex. 7, Ex. 8, Ex. 9, Ex. 10, Ex. 11, Ex. 12, Ex. 13, Ex. 14.

Lorsque le groupe est (Z/mZ, +), la suite de Fibonacci obtenue est la même que celle vue plus haut, ses éléments sont les restes des quotients eucliiens des F(n) par m. (les F(n)%m en notation des langages informatique).
Pour d'autres groupes G, en particulier les groupes finis, les suites de Fibonacci généralisées, sont définies par les conditions initiales F(0)=a, F(1)=b où a et b sont deux éléments du groupe G et pour n>1 par la même relation de récurrence F(n) = F(n-1)+F(n-2).
Lorsque le groupe est fini, la suite obtenue est périodique.

En musiquez,Xenakis utilisa la suite de Fibonacci et le groupe de rotations du cube.