/ Accueil / Arithmétique / Symboles de Legendre et Jacobi
Réciprocité quadratique - Symboles de Legendre et de Jacobi
[Legendre Voir/Cacher]

[Propriétés Voir/Cacher]
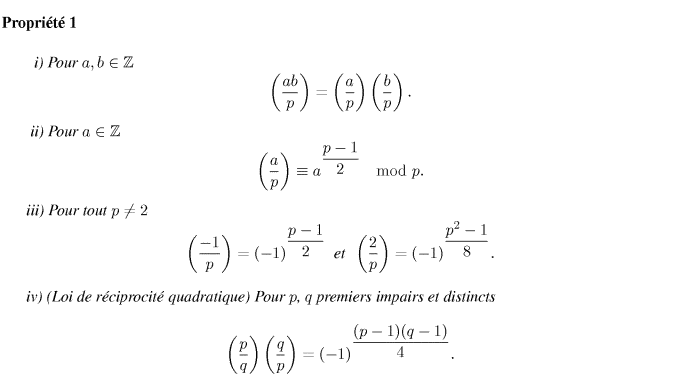
[Jacobi Voir/Cacher]
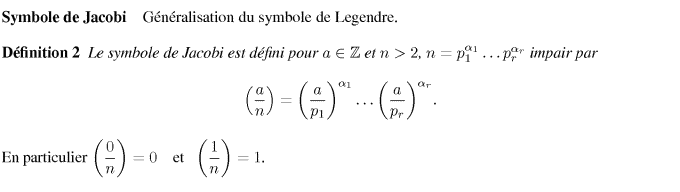
[Propriétés Voir/Cacher]
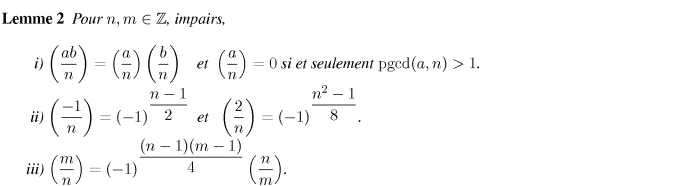

[Propriétés Voir/Cacher]
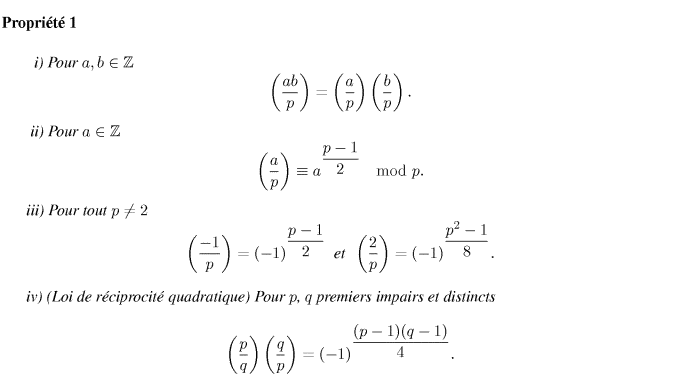
[Jacobi Voir/Cacher]
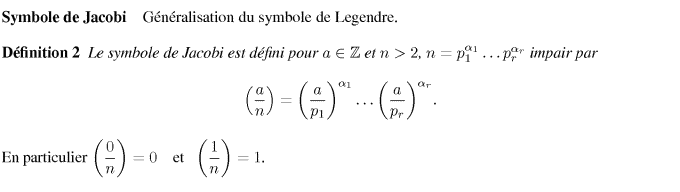
[Propriétés Voir/Cacher]
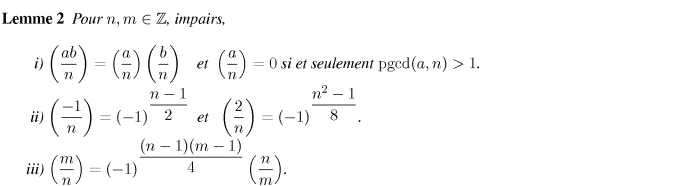
Application
L'application ci-dessous ne calcule
[Propriétés Voir/Cacher]

Lorsque
Schématiquement : Résidu quadratique => jacobi = 1 jacobi = -1 => non résidu
jacobi = -1 => non résidu
L'équivalence est vraie pour le symbole de Legendre, lorsque
jacobi(n, m) que lorsque m est impair.
[Propriétés Voir/Cacher]

Lorsque
jacobi(n, m)=1, l'application cherche à voir si n est un carré ou non (en calculant les carrés), ce qui permet de trouver des contre-exemples où le symbole de jacobi vaut 1 et n n'est pas un carré mod m, par exemple jacobi(483, 247) ou jacobi(941, 6713)
Schématiquement : Résidu quadratique => jacobi = 1
L'équivalence est vraie pour le symbole de Legendre, lorsque
m est premier impair.
Tableau de résidus quadratiques
La table permet de voir en premier lieu les résidus quadratiques marqués "x" :
les couples (n, b) tels que b (b en ordonnée) soit résidu quadratique mod n (n en abscisse) sont marqués dans le tableau par un "x". Il s'agit de l'ensemble des couples (n, b), n>1, b>0, tels qu'il existe x vérifiant t2 = b mod n.
Les autres couples couples pour lesquels le symbole de jacobi vaut +1 sans que b ne soit résidu quadratique mod n sont marqués "1", et lorsque le symbole vaut 0, ils sont marqués "o". (Pour n impair uniquement).
[Table : Voir/Cacher]

les couples (n, b) tels que b (b en ordonnée) soit résidu quadratique mod n (n en abscisse) sont marqués dans le tableau par un "x". Il s'agit de l'ensemble des couples (n, b), n>1, b>0, tels qu'il existe x vérifiant t
Les autres couples couples pour lesquels le symbole de jacobi vaut +1 sans que b ne soit résidu quadratique mod n sont marqués "1", et lorsque le symbole vaut 0, ils sont marqués "o". (Pour n impair uniquement).
[Table : Voir/Cacher]

Documents - références - compléments - liens utiles

Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


