Accueil / Mots / Combinatoire / Chiffres à l'ordre près
Chiffres décimaux à l'ordre d'écriture près
Naturels ayant les mêmes chiffres
Nombre d'écritures différentes
Les chiffres des deux nombres 385800 et 508083 sont les mêmes, mais ils sont placés différemment.
Combien de nombres différents peut-on obtenir avec ces mêmes chiffres ?
(Il ne serait pas correct d'écrire 038058, qui ne serait pas compté. Ce nombre est en réalité 38058 et n'a donc que cinq chiffres).
Le premier chiffre à partir de la gauche est donc nécessairement différent de zéro.
Combien de nombres différents peut-on obtenir avec ces mêmes chiffres ?
(Il ne serait pas correct d'écrire 038058, qui ne serait pas compté. Ce nombre est en réalité 38058 et n'a donc que cinq chiffres).
Le premier chiffre à partir de la gauche est donc nécessairement différent de zéro.
Dénombrement
Lorsque vous regardez les chiffres d'un type particulier — les deux chiffres 8 par exemple — dans les écritures décimales 385800, 508083, 830508, etc. ces chiffres occupent deux
positions quelconques * 8 * 8 * * ou * * 8 * 8 * ou 8 * * * * 8 et bien d'autres encore (15 en tout) d'un ensemble de six positions possibles. Si au contraire on observe les deux 0, ceux-ci ne peuvent se placer qu'en cinq positions et non six, ils ne peuvent être le chiffre de gauche, (cette restriction ne concerne que les zéros).
En notant n0, n1, n2, ..., n9 les effectifs des chiffres dans le nombre N de n = n0 + n1 + ... + n9 chiffres, la recherche de toutes les écritures possibles de N, se ramène aux choix successifs d'un sous-ensemble de n0 zéros parmi (n-1) places, puis de n1 chiffres 1 parmi (n-n0) emplacements ... jusqu'à placer un n9 chiffres 9 aux n9 positions encore vides.
Les nombres de combinaisons de p éléments parmi n seront notés C(n, p) ou binomial(n, p).
Le nombre d'écritures différentes possibles est donc C(n-1, n0) × C(n-n0, n0) × C(n-n0-n1, n1) ×... C(n-n0-n1-...8, n6).
Ce nombre est égal à (n-1)! × (n-n0+1) /(n0! n1! n2! ... n9!)
En notant n0, n1, n2, ..., n9 les effectifs des chiffres dans le nombre N de n = n0 + n1 + ... + n9 chiffres, la recherche de toutes les écritures possibles de N, se ramène aux choix successifs d'un sous-ensemble de n0 zéros parmi (n-1) places, puis de n1 chiffres 1 parmi (n-n0) emplacements ... jusqu'à placer un n9 chiffres 9 aux n9 positions encore vides.
Les nombres de combinaisons de p éléments parmi n seront notés C(n, p) ou binomial(n, p).
Le nombre d'écritures différentes possibles est donc C(n-1, n0) × C(n-n0, n0) × C(n-n0-n1, n1) ×... C(n-n0-n1-...8, n6).
Ce nombre est égal à (n-1)! × (n-n0+1) /(n0! n1! n2! ... n9!)
Partages, multi-ensembles et coefficients multinomiaux
2) Anagrammes Quel est le nombre d'écritures différentes, en changeant l'ordre des éléments, du multi ensemble ? Quel sont les nombres d'anagrammes des mots "bonbonne" ou "combinatoire", "invitation", "transcendance", "illusion", "bavardage", "avatar", "iriser", "illisible"
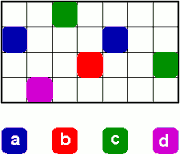
3) Partager ce rectangle. De combien de manières différentes pouvez-vous colorier les 28 cases du rectangle ci-contre, si vous connaissez les nombres 7, 4, 9, 8, de cases de chacune des quatre couleurs ?
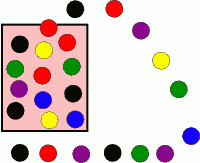
4) Suite finie et ordonnée. Combien d'alignements de couleurs différents peut-on obtrnir en extrayant au hasard les boules de l'urne ?

Développements décimaux et nombres d'écritures à l'ordre près des chiffres
Écritures décimales de n chiffres
Pour n = 0, 1, 2, 3, 4, ... chiffres il y a
Si on ne tient pas compte de l'ordre des chiffres, c'est-à-dire si on confond dans le décompte les entiers ayant les mêmes chiffres, on obtient la suite
Pour expliquer simplement de résultat, binomial(n+9, 9) est le nombre de manières de placer 9 séparations X qui sépareront les n chiffres (de 9 à 0) : 9 9 X 8 8 8 XX 6 X 5 5 X X X 2 2 X X 0 0 0 dans un tableau de n+9 cases. Seul le cas XXXXXXXXX000...00 où tous les n chiffres sont 0 est exclu, le nombre de solutions est donc bien binomial(n+9, 9)-1.
Ainsi, pour n=39, il n'y que 1677106639 (167 millions) choix différents des 39 chiffres décimaux pour écrire tous les 900 000 000 000 000 000 000 000 000 000 000 000 000 (neuf cent milliards de milliards de milliards de milliards) nombres de 39 chiffres.
0, 9, 90, 900, 9000, 90000, 900000, ..., 9×10n-1, ...nombres entiers naturels non nuls de n chiffres (suite A052268)
Si on ne tient pas compte de l'ordre des chiffres, c'est-à-dire si on confond dans le décompte les entiers ayant les mêmes chiffres, on obtient la suite
0, 9, 54, 219, 714, 2001, 5004, 11439, ..., binomial(n+9,9)-1, ...qui est la suite A035927. Les valeurs sont, pour n positif non nul binomial(n+9, 9)-1, Dans GP/PARI : a(n)=if(n<0,0,binomial(n+9,9)-1). Liste jusqu'à n=1000 : liste 1
Pour expliquer simplement de résultat, binomial(n+9, 9) est le nombre de manières de placer 9 séparations X qui sépareront les n chiffres (de 9 à 0) : 9 9 X 8 8 8 XX 6 X 5 5 X X X 2 2 X X 0 0 0 dans un tableau de n+9 cases. Seul le cas XXXXXXXXX000...00 où tous les n chiffres sont 0 est exclu, le nombre de solutions est donc bien binomial(n+9, 9)-1.
Ainsi, pour n=39, il n'y que 1677106639 (167 millions) choix différents des 39 chiffres décimaux pour écrire tous les 900 000 000 000 000 000 000 000 000 000 000 000 000 (neuf cent milliards de milliards de milliards de milliards) nombres de 39 chiffres.
Écritures décimales de n chiffres au plus
En cumulant les termes de la suite précédente, on obtient le nombre de multi-ensembles dont les n éléments sont pris parmi les dix chiffres de 0 à 9, (non tous des 0). C'est le nombre de manières de choisir les chiffres pour former tous les naturels non nuls de n chiffres au plus, La suite obtenue est :
On peut remarquer que somme(p=1, n, binomial(p+9,9)-1) = binomial(n+10,10)-n-1. Les logiciels de calculs formel permettent d'obtenir ce résultat, par exemple MAXIMA :
0, 9, 63, 282, 996, 2997, 8001, 19440, 43749, 92368, 184745, 352704, 646633, 1144052, 1961241, 3268744, 5311718, 8436267, 13123091, 20029990, 30044994,..., binomial(n+10,10)-n-1,...Cette suite ne semble se trouver dans OEIS. Dans GP/PARI : a(n)=if(n<0,0,binomial(n+10,0)-n-1). Liste jusqu'à n=1000 : liste 2
On peut remarquer que somme(p=1, n, binomial(p+9,9)-1) = binomial(n+10,10)-n-1. Les logiciels de calculs formel permettent d'obtenir ce résultat, par exemple MAXIMA :
(%i1) nusum(binomial(p+9,9),p,0,n);
(%o1) (n + 1) (n + 2) (n + 3) (n + 4) (n + 5) (n + 6) (n + 7) (n + 8) (n + 9)
(n + 10)/3628800
Vous pouvez télécharger le livre A = B de Marko Petkovsek, Herbert Wilf et Doron Zeilberger si vous devez utiliser ces sommes binomiales et plus généralement savoir ce que peut apporter l'ordinateur pour résoudre ces calculs formels de combinatoire.
Pour un premier contact, [utilisez ce formulaire] ou recopiez l'adresse qui y figure. Merci d'indiquer la page précise "http://jeux-et-mathématiques.davalan.org/" de la page du site, cela m'aidera et évitera toute confusion. Ne joignez aucun document.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès maintenant et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès maintenant et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


