Accueil |
Index Graphes |
Cours BTS |
Circuit eulérien |
Plus court chemin |
Nombre chromatique |
Matrice de transition
Graphes probabilistes (Matrices de transition)
Calculs
On peut effectuer les calculs matriciels suivants :
1) Le produit P0 M du vecteur ligne P0 par la matrice carrée M. On obtient alors le vecteur P1 = P0 M
2) L'élévation de la matrice M à une puissance n. On obtient Mn
3) On peut combiner ces deux types de calculs pour obtenir P0 Mn = Pn
Remarque : Le vecteur P0 et la matrice M doivent avoir même dimension n pour pouvoir se correspondre. M aura n lignes et n colonnes. Dans l'exemple on a n=3 mais d'autres exemples et d'autres dimensions sont évidemment possibles.
1) Le produit P0 M du vecteur ligne P0 par la matrice carrée M. On obtient alors le vecteur P1 = P0 M
2) L'élévation de la matrice M à une puissance n. On obtient Mn
3) On peut combiner ces deux types de calculs pour obtenir P0 Mn = Pn
Remarque : Le vecteur P0 et la matrice M doivent avoir même dimension n pour pouvoir se correspondre. M aura n lignes et n colonnes. Dans l'exemple on a n=3 mais d'autres exemples et d'autres dimensions sont évidemment possibles.
Exemples
Maladie
Dans l'exemple, on considère qu'une personne est dans l'un des trois états : A elle est immunisée, B elle est malade,
C elle n'est ni malade ni immunisée.
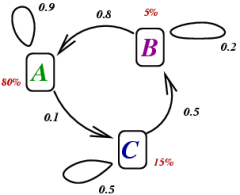
On admet que d'un mois au suivant, son état peut changer selon les règles ci-dessous.
(1ère ligne de la matrice)
A vers A : elle est immunisée et reste immunisée avec la probabilité 0,9.
A vers C : elle est immunisée et passe à l'état C avec la probabilité 0,1.
(2ème ligne de la matrice)
B vers A : elle cesse d'être malade et est immunisée avec la probabilité 0,8.
B vers B : elle reste malade avec la probabilité 0,2
(3ème ligne de la matrice)
C vers B : elle n'était ni malade ni immunisée et devient malade avec une probabilité 0,5
C vers C : elle reste dans l'état C avec la probabilité 0,5.
P0 = (0,8; 0,05; 0,15) sigifie qu'i y a à cet instant 80 % d'immunisés, 5 % de personnes malades et 15 % de personnes non immunisées et non malades.
En calculant P1, P2, ... on peut suivre l'évolution de la maladie dans la population mois après mois.

On admet que d'un mois au suivant, son état peut changer selon les règles ci-dessous.
(1ère ligne de la matrice)
A vers A : elle est immunisée et reste immunisée avec la probabilité 0,9.
A vers C : elle est immunisée et passe à l'état C avec la probabilité 0,1.
(2ème ligne de la matrice)
B vers A : elle cesse d'être malade et est immunisée avec la probabilité 0,8.
B vers B : elle reste malade avec la probabilité 0,2
(3ème ligne de la matrice)
C vers B : elle n'était ni malade ni immunisée et devient malade avec une probabilité 0,5
C vers C : elle reste dans l'état C avec la probabilité 0,5.
P0 = (0,8; 0,05; 0,15) sigifie qu'i y a à cet instant 80 % d'immunisés, 5 % de personnes malades et 15 % de personnes non immunisées et non malades.
En calculant P1, P2, ... on peut suivre l'évolution de la maladie dans la population mois après mois.
Pièce de monnaie
Énoncé
Quelle est la probabilité, en 100 lancers d'une pièce de monnaie bien équilibrée, d'obtenir au moins une fois six résultats consécutifs identiques (ou plus) ?
Graphe et matrice de transition
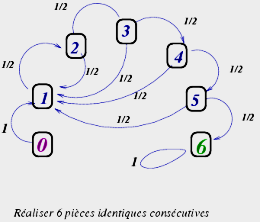
Le graphe a six principaux sommets 1, 2, ..., 6. On peut, pour simplifier, ne pas considérer le sommet 0 car dès le premier lancer, il ne sera plus jamais utilisé.
Lorsqu'on est dans l'état k < 6 on passe à l'état k+1 avec la probabilité 1/2 si le résultat est identique au précédent, mais on revient à l'état 1 avec la même probabilité 1/2 lorsque le résultat est différent.
Une fois dans l'état 6 on reste dans cet état quelque soit le résultat suivant : 'on a obtenu au moins une fois six coups successifs identiques'.
La matrice de transition A et le vecteur P_1 (et non P_0) sont
A = 0.5 0.5 0 0 0 0
0.5 0 0.5 0 0 0
0.5 0 0 0.5 0 0
0.5 0 0 0 0.5 0
0.5 0 0 0 0 0.5
0 0 0 0 0 1
P_1 = (1 0 0 0 0 0)
P_100 = P_1 * A99
La solution est donnée par le calcul de P_100 = P_1 * A^99.
La probabilité cherchée est un peu supérieure à 0,80 = 80 %
Variante : k PILES successifs en N lancers
Problème :Déterminer la probabilité d'obtenir au moins k "PILES" consécutifs en lançant N fois une pièce de monnaie.
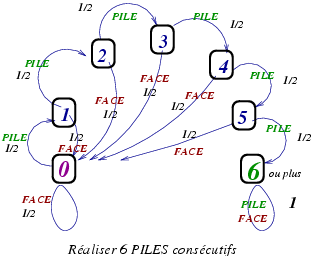
Les k+1 sommets du graphe correspondent à 0, 1, 2, ..., k PILES ou plus et la matrice M de transition est d'ordre k+1, le vecteur P0=[1, 0, 0...] donne l'état à l'instant 0 et Pk= P0 × Mk à l'instant k.

Les k+1 sommets du graphe correspondent à 0, 1, 2, ..., k PILES ou plus et la matrice M de transition est d'ordre k+1, le vecteur P0=[1, 0, 0...] donne l'état à l'instant 0 et Pk= P0 × Mk à l'instant k.
Les probabilités P(N, k) se trouvent dans le tableau ci-dessous. N se lit sur la ligne supérieure du tableau et k dans la colonne de gauche. Les fractions sont réduites, elles sont les valeurs exactes des probabilités.
| P(N, k) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 0 | : | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | : | 0 | 1/2 | 3/4 | 7/8 | 15/16 | 31/32 | 63/64 | 127/128 | 255/256 | 511/512 | 1023/1024 | 2047/2048 | 4095/4096 | 8191/8192 | 16383/16384 | 32767/32768 | 65535/65536 | 131071/131072 | 262143/262144 | 524287/524288 | 1048575/1048576 |
| 2 | : | 0 | 0 | 1/4 | 3/8 | 1/2 | 19/32 | 43/64 | 47/64 | 201/256 | 423/512 | 55/64 | 1815/2048 | 3719/4096 | 3791/4096 | 15397/16384 | 31171/32768 | 7869/8192 | 126891/131072 | 255379/262144 | 256671/262144 | 1030865/1048576 |
| 3 | : | 0 | 0 | 0 | 1/8 | 3/16 | 1/4 | 5/16 | 47/128 | 107/256 | 119/256 | 65/128 | 1121/2048 | 2391/4096 | 79/128 | 1327/2048 | 22159/32768 | 46023/65536 | 47591/65536 | 49033/65536 | 402873/524288 | 825259/1048576 |
| 4 | : | 0 | 0 | 0 | 0 | 1/16 | 3/32 | 1/8 | 5/32 | 3/16 | 111/512 | 251/1024 | 279/1024 | 153/512 | 83/256 | 5713/16384 | 12199/32768 | 809/2048 | 6831/16384 | 7177/16384 | 240335/524288 | 501239/1048576 |
| 5 | : | 0 | 0 | 0 | 0 | 0 | 1/32 | 3/64 | 1/16 | 5/64 | 3/32 | 7/64 | 255/2048 | 571/4096 | 631/4096 | 345/2048 | 187/1024 | 805/4096 | 27553/131072 | 58631/262144 | 3881/16384 | 32751/131072 |
| 6 | : | 0 | 0 | 0 | 0 | 0 | 0 | 1/64 | 3/128 | 1/32 | 5/128 | 3/64 | 7/128 | 1/16 | 575/8192 | 1275/16384 | 1399/16384 | 761/8192 | 411/4096 | 1765/16384 | 1885/16384 | 128257/1048576 |
| 7 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/128 | 3/256 | 1/64 | 5/256 | 3/128 | 7/256 | 1/32 | 9/256 | 1279/32768 | 2811/65536 | 3063/65536 | 1657/32768 | 891/16384 | 3813/65536 |
| 8 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/256 | 3/512 | 1/128 | 5/512 | 3/256 | 7/512 | 1/64 | 9/512 | 5/256 | 2815/131072 | 6139/262144 | 6647/262144 | 3577/131072 |
| 9 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/512 | 3/1024 | 1/256 | 5/1024 | 3/512 | 7/1024 | 1/128 | 9/1024 | 5/512 | 11/1024 | 6143/524288 | 13307/1048576 |
| 10 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/1024 | 3/2048 | 1/512 | 5/2048 | 3/1024 | 7/2048 | 1/256 | 9/2048 | 5/1024 | 11/2048 | 3/512 |
| 11 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/2048 | 3/4096 | 1/1024 | 5/4096 | 3/2048 | 7/4096 | 1/512 | 9/4096 | 5/2048 | 11/4096 |
| 12 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/4096 | 3/8192 | 1/2048 | 5/8192 | 3/4096 | 7/8192 | 1/1024 | 9/8192 | 5/4096 |
| 13 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/8192 | 3/16384 | 1/4096 | 5/16384 | 3/8192 | 7/16384 | 1/2048 | 9/16384 |
| 14 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/16384 | 3/32768 | 1/8192 | 5/32768 | 3/16384 | 7/32768 | 1/4096 |
| 15 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/32768 | 3/65536 | 1/16384 | 5/65536 | 3/32768 | 7/65536 |
| 16 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/65536 | 3/131072 | 1/32768 | 5/131072 | 3/65536 |
| 17 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/131072 | 3/262144 | 1/65536 | 5/262144 |
| 18 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/262144 | 3/524288 | 1/131072 |
| 19 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/524288 | 3/1048576 |
| 20 | : | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/1048576 |
Références, ressources, liens
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


