

Pavages rythmiques parfaits III
Recherche d'une clique maximum
Graphes
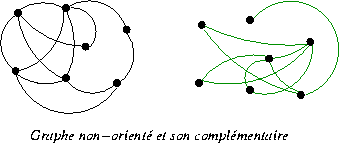
Graphe non orienté et son complémentaire
Un graphe orienté G=(X, E) est défini par l'ensemble X de ses sommets et par un sous-ensemble E de X2.
E est l'ensemble des arcs du graphe. L'ordre du graphe est le nombre |X| de ses sommets.
Une matrice d'incidence du graphe A = [aij] est telle que [aij est égal à 1 ou à 0 selon que (xi, xj) est un arc du graphe ou ne l'est pas.
Lorsque l'existence de tout arc (xi, xk) entraîne celle de (xk, xi), le graphe est symétrique et peut être considéré comme un graphe non orienté, on confond les deux arcs (xi, xk) et (xk, xi) en une seule arête xixk
Le graphe G', complémentaire du graphe non-orienté G a même ensemble de sommets que G (voir figure) et contient toutes les arêtes qui ne sont pas dans G (les boucles sont généralement omises).
Dans ce qui suit on ne considère plus que des graphes non-orientés sans boucles.
E est l'ensemble des arcs du graphe. L'ordre du graphe est le nombre |X| de ses sommets.
Une matrice d'incidence du graphe A = [aij] est telle que [aij est égal à 1 ou à 0 selon que (xi, xj) est un arc du graphe ou ne l'est pas.
Lorsque l'existence de tout arc (xi, xk) entraîne celle de (xk, xi), le graphe est symétrique et peut être considéré comme un graphe non orienté, on confond les deux arcs (xi, xk) et (xk, xi) en une seule arête xixk
Le graphe G', complémentaire du graphe non-orienté G a même ensemble de sommets que G (voir figure) et contient toutes les arêtes qui ne sont pas dans G (les boucles sont généralement omises).
Dans ce qui suit on ne considère plus que des graphes non-orientés sans boucles.
Clique maximum
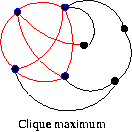
Un graphe G est dit complet lorsque deux sommets quelconques différents sont toujours reliés.
Une clique C du graphe G est un sous-graphe complet C(Y, F) du graphe G(X, E) c.-à-d. Y est un sous-ensemble de X, F est un sous-ensemble de E et C est complet.
Une clique est maximum lorsqu'il n'existe pas de clique ayant plus de sommets.
Une clique C du graphe G est un sous-graphe complet C(Y, F) du graphe G(X, E) c.-à-d. Y est un sous-ensemble de X, F est un sous-ensemble de E et C est complet.
Une clique est maximum lorsqu'il n'existe pas de clique ayant plus de sommets.
Application aux pavages rythmiques
Un pavage rythmique parfait est une clique maximum
Le pavage E C B D B C B E D C A A A D E de longueur 15 est formé des cinq progressions arithmétiques A, B, C, D, E, de trois termes chacune et de raisons 1, 2, 4, 5, 7 dont les premiers éléments valent respectives 10, 2, 1, 3, 0, (les rangs des lettres A, B, C, D, E dans
la chaîne ECBDBCBEDCAAADE)
Ces cinq progressions ont été choisies parmi les 49 possibles. Toutes ces 49 progressions possibles de raisons supérieures ou égales à 1, diffèrent par l'un au moins de leurs termes, elles sont représentées par les sommets du graphe non orienté ci-dessous et notées S_1, ..., S_49.
Les arêtes de ce graphe joignent des progressions compatibles (n'ayant aucun élément commun). Le nombre des arêtes du est de 414.
Trouver un pavage de longueur 15 se ramène à la détermination d'une clique de 5 sommets. Cette clique est nécessairement maximum. Ce graphe ne possède que deux cliques maximum, cliquez l'image pour l'obtenir au format A4.

Clique d'un graphe
Les segments de couleur rouge sont des arêtes du graphe
Le graphe 17x3 possède 625 sommets et 151704 arêtes, le nombre de ses cliques est de plus de 141 millions. J'ai bien essayé de construire la figure mais LATEX en a décidé autrement :
Quelques graphes
Ces cinq progressions ont été choisies parmi les 49 possibles. Toutes ces 49 progressions possibles de raisons supérieures ou égales à 1, diffèrent par l'un au moins de leurs termes, elles sont représentées par les sommets du graphe non orienté ci-dessous et notées S_1, ..., S_49.
Les arêtes de ce graphe joignent des progressions compatibles (n'ayant aucun élément commun). Le nombre des arêtes du est de 414.
Trouver un pavage de longueur 15 se ramène à la détermination d'une clique de 5 sommets. Cette clique est nécessairement maximum. Ce graphe ne possède que deux cliques maximum, cliquez l'image pour l'obtenir au format A4.

Clique d'un graphe
Les segments de couleur rouge sont des arêtes du graphe
Le graphe 17x3 possède 625 sommets et 151704 arêtes, le nombre de ses cliques est de plus de 141 millions. J'ai bien essayé de construire la figure mais LATEX en a décidé autrement :
! TeX capacity exceeded, sorry [main memory size=263001].
Il est vrai qu'à raison d'une ligne par arête du graphe, le fichier était un peu grand.
| n\k | k=3 | k=4 | k=5 | k=6 |
| n=4 | 4x3 | 4x4 | 4x5 | 4x6 |
| n=5 | 5x3 | 5x4 | 5x5 | 5x6 |
| n=6 | 6x3 | 6x4 | 6x5 | 6x6 |
| n=7 | 7x3 | 7x4 | 7x5 | 7x6 |
Quelques graphes
Graphe d'intersection
Le graphe non orienté dont l'ensemble S des sommets a pour éléments les sous-ensembles de E =
{0, 1, ..., k*n-1} formés de k éléments en progression arithmétique et dont les arêtes relient deux sous-ensembles dont l'intersection n'est pas vide est un graphe d'intersection.
Ce graphe est le graphe complémentaire du graphe étudié au paragraphe précédent.
Trouver un pavage rythmique parfait de n progressions de longueurs k revient à trouver dans le graphe un sous-ensemble stable de n sommets (tels qu'on ne puisse trouver deux d'entre-eux reliés par une arête du graphe).
On peut voir que dans ce graphe il est impossible d'obtenir un sous-ensemble stable de plus de n sommets (car il n'y a que k*n éléments dans E). Un sous-ensemble stable maximum ne peut donc pas avoir plus de n sommets et trouver un pavage rythmique parfait revient à trouver un sous-ensemble stable maximum de n sommets.

Stable maximum d'un graphe d'intersection
Les segments de couleur rouge ne sont pas des arêtes du graphe
Ce graphe est le graphe complémentaire du graphe étudié au paragraphe précédent.
Trouver un pavage rythmique parfait de n progressions de longueurs k revient à trouver dans le graphe un sous-ensemble stable de n sommets (tels qu'on ne puisse trouver deux d'entre-eux reliés par une arête du graphe).
On peut voir que dans ce graphe il est impossible d'obtenir un sous-ensemble stable de plus de n sommets (car il n'y a que k*n éléments dans E). Un sous-ensemble stable maximum ne peut donc pas avoir plus de n sommets et trouver un pavage rythmique parfait revient à trouver un sous-ensemble stable maximum de n sommets.

Stable maximum d'un graphe d'intersection
Les segments de couleur rouge ne sont pas des arêtes du graphe
Recherche d'une clique
Format DIMACS
Pour que différentes équipes de recherche puissent tester leurs logiciels sur les mêmes graphes ceux-ci sont généralements écrits dans un fichier au format DIMACS texte ou binaire, (ce dernier est préférable lorsque la densité des arêtes est supérieure à 1,2%).
Le programme tomj2dimacs.c permet d'écrire dans le format binaire les graphes relatifs aux pavages rythmiques parfaits.
Pour utiliser le programme faire :
Deux fichiers
Le premier contient le graphe, le second contient des lignes comme celle-ci :
Les programmes de conversion entre les formats de fichiers texte et binaire se trouvent dans l'archive binformat.shar placée dans le [répertoire] Dimacs à l'université Rutgers. (Ou aller à : The Second DIMACS Implementation Challenge: 1992-1993).
Les programmes de conversion entre les fichiers texte et binaires sont dans binformat.shar dans ce [répertoire Dimacs].
Le programme bin2asc permet de passer du format binaire au format texte. Le programme asc2bin fait l'inverse.
Par exemple :

permet de construire le fichier tomj5_3.clg.b

permet ensuite d'obtenir tomj5_3.clg au format texte
Le programme tomj2dimacs.c permet d'écrire dans le format binaire les graphes relatifs aux pavages rythmiques parfaits.
Pour utiliser le programme faire :
tomj2dimacs 15 4 (lorsque n=15 et k=4).
Deux fichiers
tomj.clg15_4.b et nodes15_4 seront écrits.
Le premier contient le graphe, le second contient des lignes comme celle-ci :
c 532 6 15 où l'on voit que le sommet 532 correspond à la progression (6, 6+15, 6+2*15, 6+3*15) de premier terme 6 et de raison 15.
Les programmes de conversion entre les formats de fichiers texte et binaire se trouvent dans l'archive binformat.shar placée dans le [répertoire] Dimacs à l'université Rutgers. (Ou aller à : The Second DIMACS Implementation Challenge: 1992-1993).
Les programmes de conversion entre les fichiers texte et binaires sont dans binformat.shar dans ce [répertoire Dimacs].
Le programme bin2asc permet de passer du format binaire au format texte. Le programme asc2bin fait l'inverse.
Par exemple :
tomj2dimacs 5 3
permet de construire le fichier tomj5_3.clg.b
bin2asc tomj5_3.clg.b
permet ensuite d'obtenir tomj5_3.clg au format texte
Logiciels utilisés
Les logiciels d'auteurs différents, répertoriés ci-dessous peuvent être facilement téléchargés sur leurs sites respectifs, installés puis utilisés pour rechercher des cliques dans les graphes qui nous intéressent.
Ces programmes qui recherchent une clique maximum lisent les graphes soit au format texte soit au format binaire.
Les liens qui permettent de les télécharger sont indiqués au bas de cette page.
 rls (Reactive Local Search for Maximum Clique) de R. Battiti and M. Protasi.
rls (Reactive Local Search for Maximum Clique) de R. Battiti and M. Protasi.
Rls lit les fichiers au format texte et a trouve aisément une clique maximum pour n=15 et k=4.
Rls est utilisable en ligne sur son site.
On peut soit écrire le graphe au format texte, soit indiquer l'emplacement sur son ordinateur du fichier texte ou binaire qui contient ce graphe.
Vous pouvez tester Rls en téléchargeant au préalable sur votre ordinateur le fichier tomj.clg5_3 ou tomj.clg5_3.b. Choisissez un temps de calcul de 10 s ou de 60s.
Rls trouvera une clique maximum (par exemple 11 16 35 44 49) et construira deux graphiques.
Vous pouvez aussi essayer de déterminer les cliques maximum des graphes tomj.clg7_3.b, tomj.clg8_3.b, tomj.clg9_3.b.
Choisissez une durée de 60s pour obtenir une clique maximum avec le fichier tomj.clg15_4.b (10 59 159 182 245 264 336 354 401 438 481 523 532 541 566).
Vous pouvez ensuite déterminer le pavage correspondant à la clique trouvée au paragraphe suivant.
 qualex-ms de Stanislav Busygin.
qualex-ms de Stanislav Busygin.
Ces programmes qui recherchent une clique maximum lisent les graphes soit au format texte soit au format binaire.
Les liens qui permettent de les télécharger sont indiqués au bas de cette page.
Rls lit les fichiers au format texte et a trouve aisément une clique maximum pour n=15 et k=4.
Rls est utilisable en ligne sur son site.
On peut soit écrire le graphe au format texte, soit indiquer l'emplacement sur son ordinateur du fichier texte ou binaire qui contient ce graphe.
Vous pouvez tester Rls en téléchargeant au préalable sur votre ordinateur le fichier tomj.clg5_3 ou tomj.clg5_3.b. Choisissez un temps de calcul de 10 s ou de 60s.
Rls trouvera une clique maximum (par exemple 11 16 35 44 49) et construira deux graphiques.
Vous pouvez aussi essayer de déterminer les cliques maximum des graphes tomj.clg7_3.b, tomj.clg8_3.b, tomj.clg9_3.b.
Choisissez une durée de 60s pour obtenir une clique maximum avec le fichier tomj.clg15_4.b (10 59 159 182 245 264 336 354 401 438 481 523 532 541 566).
Vous pouvez ensuite déterminer le pavage correspondant à la clique trouvée au paragraphe suivant.
Retrouvez le pavage
Retrouvez le pavage qui correspond à la clique obtenue par l'un des logiciels ci-dessus.
Indiquez les deux valeurs de 'n' (nombre de progressions à placer) et de 'k' (longueur des progressions arithmétiques).
Indiquez aussi les codes des sommets, ils sont au nombre de 'n' au plus.
Lorsque le nombre de sommets est inférieur à 'n', le pavage est incomplet et certaines places sont marquées d'un '_'.
 Clique - Implementations The Stony Brook Algorithm Repository Steven S. Skiena
Clique - Implementations The Stony Brook Algorithm Repository Steven S. Skiena
 Stas Busygin's NP-Completeness Page
Stas Busygin's NP-Completeness Page
 InterTools -- Max Clique R. Battiti and M. Protasi.
InterTools -- Max Clique R. Battiti and M. Protasi.
 nmclique from Matula and Johri
nmclique from Matula and Johri
 A Journey through Intersection Graph County Erich Prisner
A Journey through Intersection Graph County Erich Prisner
 Sculpture à l'IHÉS l'Institut possède une représentation d'une des suites de Skolem sous forme de sculpture, réalisée par l'artiste américaine Jessica Stockholder, suivant un cahier des charges établi par des classes de primaire qui ont travaillé sur le jeu des cavaliers.
Sculpture à l'IHÉS l'Institut possède une représentation d'une des suites de Skolem sous forme de sculpture, réalisée par l'artiste américaine Jessica Stockholder, suivant un cahier des charges établi par des classes de primaire qui ont travaillé sur le jeu des cavaliers.


|Définitions, exemples| |Construction, programmes| |Graphes et hypergraphes| |Pavages infinis ou mixtes ou circulaires|

Indiquez les deux valeurs de 'n' (nombre de progressions à placer) et de 'k' (longueur des progressions arithmétiques).
Indiquez aussi les codes des sommets, ils sont au nombre de 'n' au plus.
Lorsque le nombre de sommets est inférieur à 'n', le pavage est incomplet et certaines places sont marquées d'un '_'.
Exemples :
1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 .
1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 .
Liens


|Définitions, exemples| |Construction, programmes| |Graphes et hypergraphes| |Pavages infinis ou mixtes ou circulaires|
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()


